設一函數 f(x) 在 n+1 個點 x0,x1,…,xn 的值為已知。這可能是查表或由實驗方法得到的,我們常常希望知道 f(x) 在另外一點 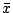 的值 的值 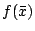 。
如果 f(x) 是 n 次多項式,那麼 。
如果 f(x) 是 n 次多項式,那麼 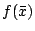 便可用補間法求得,如果 f(x) 不是 n 次多項式呢?
我們常常把 f(x) 假想成 n 次多項式 t(x),計算
便可用補間法求得,如果 f(x) 不是 n 次多項式呢?
我們常常把 f(x) 假想成 n 次多項式 t(x),計算 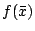 的值。
用來當作 的值。
用來當作 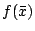 ,那麼從公式(*)知所得的誤差便是 R 項。
但 R 會不會比較小呢?讓我們從一個實例來看: ,那麼從公式(*)知所得的誤差便是 R 項。
但 R 會不會比較小呢?讓我們從一個實例來看:
設
下表列出一些 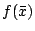 及對不同分法所得的 及對不同分法所得的 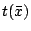 的值 的值
| 橫座標 |
1.02 |
2.34 |
3 |
3.88 |
4.15 |
4.91 |
| 縱座標 |
.490100 |
.154426 |
.100000 |
.062288 |
.054877 |
.039282 |
| 間隔數 |
補 |
|
間 |
|
法 |
|
| 2 |
.959985 |
.789400 |
.653846 |
.420985 |
.337596 |
.072765 |
| 3 |
.282394 |
.237239 |
.201357 |
.139718 |
.117644 |
.047542 |
| 5 |
.497362 |
.245889 |
.100000 |
.-039084 |
-.054607 |
.015979 |
| 8 |
.549575 |
.095381 |
.304934 |
.-088744 |
-.493703 |
-.436237 |
| 13 |
.504128 |
.180056 |
.059542 |
.210689 |
.138629 |
-.719234 |
| 21 |
.487368 |
.160295 |
.088963 |
-.131822 |
.430804 |
-16.8226 |
| 34 |
.490012 |
.154238 |
.108813 |
-.824165 |
3.45266 |
10063.8 |
| 50 |
.487850 |
.154304 |
.100000 |
6.75082 |
13.3392 |
-4418379 |
觀察這表我們可以看出當 x 趨近於 0 時,誤差實在不大,但當 x=4.91 時,誤差隨分點數增加到不可言喻的程度,所以用補間法求近似值,雖屬可行,但未必有把握行得到。到底在什麼條件下才行得通呢?這還是數學上一個沒有完全解決的問題。
|