| |
�M�ɶ����D�ܦ����Y���@���[���O�t��(difference quotient �� divided difference),
�] x0,x1,�K,xn �O��⤣�P���@���ơA�A�] f(x) �O��@�� x �ȳ����N�q����ơC�O
�h fi(x) �s f(x) ���� xi ���@���t�ӡA�q�ѪR�X���[�I�ӬݡAfi(x) ���ܳs�� (xi,f(xi)) �M (x,f(x)) ���I�����u���ײv�A��@�� 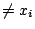 �� x �ȡAfi(x) ���O���N�q���C �� x �ȡAfi(x) ���O���N�q���C
�ڭ̥i�H�@ fi ���@���t��
�o�s�@ f(x) ���G���t�ӡA���F xi,xj ���I�H�~�Afi,j(x) �����N�q�C�馹�ڭ̥i�H�@ f(x) ���v�������t��
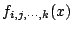 �C �C
�� 0,1,2,�K �̦��@�s���� (subscript)�A�i�H�N f(x) ���v���t�ӱƦ��U�C�ϧΡG
�o�˪��ϧΥs f ���t�Ӫ� (lozenge diagram)�A�����ĤT��H��C�����O�䥪��@���P�Ӷ��Ҧb�泻�W�@�����t�Q�̥�������������ӡC�Ҧp
�q�v���t�Ӫ��w�q�ڭ̥i�H�o��
����
�{�b���ڭ̬ݤ@�� x,x2,x3 ���� 0,2,7,-3,8 ���I���t�Ӫ��G
�q�o�Ǫ����[��A�ڭ̥i�H�q�Q�G�p�G k>n�A�h xn ���� k ���t�ӥ��ڬ� 0�A�ƹ�W�o�O�諸�A�ڭ̥i�H�μƾ��k�Ǫk���ҩ��G
�ܩ��㪺 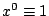 ���U���t�ӳ��O 0�A���p�ڭ̤w�g���D�w�z�� x0,x1,�K,xn-1 �����ߡA�O f(x) = xn �]�� ���U���t�ӳ��O 0�A���p�ڭ̤w�g���D�w�z�� x0,x1,�K,xn-1 �����ߡA�O f(x) = xn �]��
�O�@�� n-1 �����h�����A�ҥH f0 �� n ���H�W�t�ӳ��O 0�A�]���p�G k>n�A�h k-1>n-1�A��O
�q�Ӧ�
-
- �w�z�]���y�^ n ���h�������� n+1 ���H�W���t�ӥ��O 0�C
�{�b�^�줽��(*),���w f(x)=t(x) �O�@�� n ���h�����A�hR=0�A�H 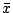 �N xn+1 �K�o �N xn+1 �K�o
�o�K�O���y���ɶ������C
�@�뻡�ӡA���y�ɶ������ä��Q���n�w�w�o�O�ѩ�s�@�t�Ӫ��ɭn�@�ܦh�����k���t�G�A���Y xi = a+ih�A�䤤 a �� h ���w�ơA�ڭ̥� yi ���� t(xi)�A�� 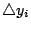 ���� yi+1 -yi�A�� ���� yi+1 -yi�A��
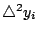 ���� ����
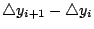 �����A�o�� �����A�o��
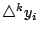 �s�@ yi ���t�� (finite differences)�A�Ӥ��y�ɶ������i�H��g�� �s�@ yi ���t�� (finite differences)�A�Ӥ��y�ɶ������i�H��g��
����
�o�s�@���y���t���ɶ������A�O�ƭȤ��R (numerical analysis) �����@�Ӱ����C
|
|
|