| |
故事講完了,現在讓我們一起研究一下孫子定理──或者中國剩餘定理。數學的發展和數字的寫法以及公式的表達法有密切的關係。中國古代盛行代數,是受了中國優良的記數法的影響。到了近代,由於人類發明 =,-,+,×,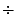 ,以及用抽象符號 x,y,a,b 代表數字,使得代數成為易懂的數學。對於「剩餘」這個概念,我們也要引進一種符號來幫助了解,記憶。 ,以及用抽象符號 x,y,a,b 代表數字,使得代數成為易懂的數學。對於「剩餘」這個概念,我們也要引進一種符號來幫助了解,記憶。
首先「三數剩二」是什麼意思呢?那不過說某一個數 x 被 3 除剩餘 2;換句話,x-2 被3整除。我們用下式表示「三數剩二」
- 定義1:
已知 a-b 被 m 整除,我們說「a、b 對模 m 同餘」。用下式(同餘式)表示。
反之,
表示「a,b 對模 m 不同餘」;換句話 a-b 不是 m 的倍數。
- 例1:
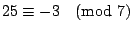
- 例2:
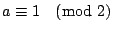 表示 a 是一個奇數。 表示 a 是一個奇數。
- 例3:
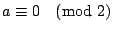 表示 a 是一個偶數。 表示 a 是一個偶數。
- 例4: 「物不知其數,三三數之剩二,五五數之剩三,七七數之剩二」可用同餘式表示如下。
「韓信點兵問題」就是求一組同餘式的公解。「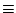 」與等式「=」有同樣的運算法則,那就是說: 」與等式「=」有同樣的運算法則,那就是說:
- 定理1:
已知
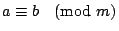 , ,
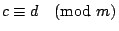 ,那麼, ,那麼,
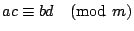 , ,
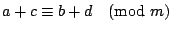 , ,
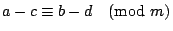 , ,
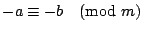 , ,
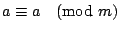 。 。
- 證明:
我們先證
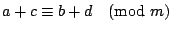 ,讀者可以仿照我們的證法,去證明其餘公式。 ,讀者可以仿照我們的證法,去證明其餘公式。
根據「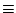 」的定義,我們知道 a-b = sm,c-d = tm 所以 」的定義,我們知道 a-b = sm,c-d = tm 所以
(a+c) - (b+d) = (a-b)+(c-d) = sm+tm = (s+t)m
那就是說,
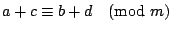 證完。 證完。
在推演孫子定理(中國剩餘定理)的過程中,我們須要一個應用兩數互質(兩數的最大公約數是1)的定理,那就是:
- 定理2:
已知 m,n 適合下式, am+bn=1,那麼 m,n 互質,反過來說,如果 m,n 互質,我們可以找到 a,b,使得
am+bn=1
- 證明:
因為 m,n 的最大公約數可以整除 am+bn,而 am+bn=1,所以 m,n 的最大公約數是1,換句話, m,n 互質。反過來說,如果己知 m,n 互質,讀者可以應用輾轉相除法,求得 a,b 使得 am+bn=1,證完。
應用定理2,我們可以解答漂母數布匹的問題了,那就是下面的定理3:
- 定理3:
己知 m,n 互質,那麼下列一組同餘式:
有公解。
- 證明:
根據定理2,我們可以找到 a,b 使得 am+bn=1,所以 bn=1-am,那麼
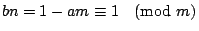 , ,
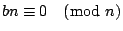 ,換句話,bn 是我們所求的一組公解,證完。 ,換句話,bn 是我們所求的一組公解,證完。
- 系1:
己知 m1 與 m2,m1 與 m3,… m1 與 mt 都互質,那麼下列一組同餘式
有公解。
- 證明:
根據已知條件,我們推論 m1 與
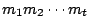 互質。在應用定理3,我們知道 互質。在應用定理3,我們知道
有公解。顯然上面那組同餘式的公解就是
的公解,證完。
- 定理4:
己知 m1,m2,…,mt 兩兩互質,並且求出 a1 是
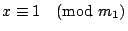 , ,
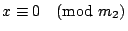 ,…, ,…,
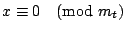 的一個公解,a2 是 的一個公解,a2 是
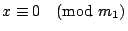 , ,
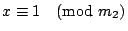 , ,
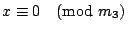 ,…, ,…,
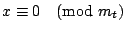 的一個公解,以此類推,求出 a3,…,at。那 的一個公解,以此類推,求出 a3,…,at。那
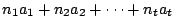 就是下列一組同餘式 就是下列一組同餘式
的一個公解。
- 證明:
我們先證明
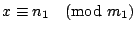 ,讀者可以仿照我們的證法,去證明其餘同餘式。 ,讀者可以仿照我們的證法,去證明其餘同餘式。
根據己知條件,我們知道
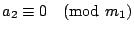 , ,
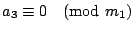 , …, , …,
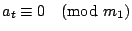 ,應用定理1,我們得出 ,應用定理1,我們得出
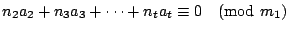 ,並且已知 ,並且已知
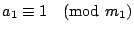 ,所以應用定理1,我們得出 ,所以應用定理1,我們得出
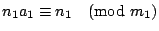 ,再應用一次定理1,我們證明 ,再應用一次定理1,我們證明
證完。
上面的定理4事實上就是孫子算經裡的解法。 a1, a2,…,at 也就是孫子算經裡面提到的「用數」。定理4再加上下面的定理5就合成了數論中的孫子定理。
- 定理5:
己知 m1,m2,…,mt 兩兩互質。並且求出 a,b 是下列一組同餘式
的兩個公解。那麼 a-b 一定是
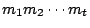 的倍數。反過來說, 的倍數。反過來說,
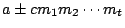 也是那一組同餘式的公解。 也是那一組同餘式的公解。
- 證明:
因為
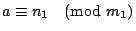 , ,
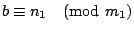 ,應用定理1,我們得到 ,應用定理1,我們得到
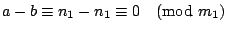 ,換句話,a-b 被 m1 整除。同樣道理 m2,…,mt 都可以整除 a-b。根據已知條件,m1,m2,…,mt 兩兩互質,所以 a-b 一定被 ,換句話,a-b 被 m1 整除。同樣道理 m2,…,mt 都可以整除 a-b。根據已知條件,m1,m2,…,mt 兩兩互質,所以 a-b 一定被
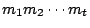 整除,那就是說,a-b 是 整除,那就是說,a-b 是
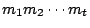 的倍數。反過來說,應用定理1, 的倍數。反過來說,應用定理1,
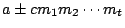 自然也是一個公解。證完。 自然也是一個公解。證完。
上面所談的都是數論的內容。如果我們把上面的定義,定理,系以及證明中的整數
m,n,a,b,m1,n1,…,等等都換成一元多項式 m(x), n(x), a(x), b(x), m1(x), n1(x), … 等等。我們就得到方程式論中的孫子定理了。
例如定理3可以改寫成:
- 定理3:
已知 m(x), n(x) 互質,那麼下列一組同餘式,
有公解。
在許多抽象數學的領域中,也有孫子定理。不過,因為牽涉的入門知識太多,這兒也就一言表過不提了。
關於孫子定理,現代數學家已有廣泛透徹的研究。讀者如果有興趣,可以參看一點數論及近代代數的書籍。這篇淺文的主要目的,也就是引起讀者對數學的興趣而已。
|
|
|