積分發展的一頁滄桑 (第 5 頁)

　1│2│3│4│5│6　

積分發展的一頁滄桑（第 5 頁）

蔡志強

首頁 | 搜尋

．原載於數學傳播第二十三卷第三期
．作者當時任教於省立板橋高中
‧對外搜尋關鍵字

五、Riemann 的就職論文

無窮小分析最重要的原理。

──J.W.R. Dedekind

不可否認 Georg Friedrich Bernhard Riemann（1826～1866）是現代數學的大師，雖然他的生命只有短暫的41年，但是，他所涉及的每一個領域，都掀起了革命性的突破。 Riemann的工作也涉及到Fourier級數，不過，Riemann當初考慮這個問題的部份原因卻是因為經濟因素。當Riemann於1851年通過他的博士論文「單複變函數一般理論基礎」答辯後，Riemann因錯失了爭取擔任Gottingen觀測台助手的機會，於是，他得轉而求取擔任沒有薪水的大學講師資格，也就是說，他的薪水是從向那些來聽他講課的學生收取學費得來的。為此，Riemann得準備一篇所謂的就職論文，而他的就職論文正是有關於Fourier級數的。恰巧在這一年（1852）的秋天，柏林大學的Dirichlet到Gottingen 度假，而Dirichlet正是這方面的專家，因此，很自然地，Riemann就向Dirichlet 請教。後來，Riemann在給他的父親信中寫道這一段經歷：「宴會之後，第二天早上，Dirichlet 和我在一起談了兩個小時，他把他的筆記給了我，而這正是我準備就職論文所需要的，否則我就要在圖書館花費大量時間進行艱苦的研究才能得到這些。他還和我一起誦讀我的論文，對我非常友好。考慮到我們之間地位的巨大差異，這是我根本不敢想像的。我希望他以後還能記得我」。然而，Riemann並沒有因此而馬上完成他的論文，因為此時的他正熱衷於數學物理的問題：一直拖到1853年底，才完成了這篇論文。或許，有人對Riemann 這樣的純數學家會熱衷於數學物理感到疑惑，其實：Riemann花在物理上的時間與純數學一樣多，甚至，在Gottingen大學的最後三個學期，他都是物理學家Wilhelm Weber的實驗室助手，而這樣的素養，使得Riemann在物理上絲毫不遜色於Newton, Einstein等大物理學家，最重要的是，這些素養使得Riemann得以作出他最出名的就職演講──「論作為幾何基礎的假設」(Über die Hypothesen welche der Geometrie zu Grunde liegen)，該講演為物理學的幾何化作了最好的準備，以迎接Einstein的到來。

Riemann在這篇「論函數通過三角級數的可表示性」(Über die Darstellbarkeit einer Funktion durch einer trigonometrische Reihe) 的就職論文前三節中，首先對 Fourier級數的歷史做了一些回顧，而這些資訊都是Dirichlet提供給Riemann的，在討論完Dirichlet的論文後，Riemann做了一個評註：「我們可以很合理的說：Dirichlet未曾分析的函數其實是不存在自然界中的」。但是，基於底下的兩個原因，促使Riemann考慮更廣泛的函數類，他寫道：

: (1)由於這項課題與無窮小分析的原理有著密切的關係，並且可以使得這些原理更加清楚與正確。
: (2)Fourier級數的應用不僅侷限於物理的應用而已；它同時已經成功地應用於許多純數學的領域之中，比如:數論，而在這些領域之中，Dirichlet未曾考慮過的函數是否可以用三角級數表示出來的問題，似乎日趨重要。

因此，Riemann為了將Dirichlet關於函數用三角級數表達的結果推廣到儘可能多的不連續函數，因此，Riemann不僅接受了Dirichlet關於函數的現代觀念，更進一步，Riemann 必須找尋比Cauchy積分更廣的積分定義，以適用於更廣泛的函數類。因此，Riemann在論文第四節的一開頭就說「我們如何了解 $\int_a^bf（x）$ 呢？」他給出了類似於Cauchy但比Cauchy更廣義的積分定義：

Riemann的積分定義

為建立此事，我們取一串介於a與b之間且按大小排列的值x₁,x₂,…,x_n。為方便起見:以 $\delta_1$ 表示x₁-a,以 $\delta_2$ 表示x₂-x₁,…,以 $\delta_n$ 表示b-x_n-1，以 $\epsilon_i$ 表示正的小數，則下列和的值

$\begin{displaymath}S=\delta_1f(a+\epsilon_1\delta_1)+\delta_2f(x_1+\epsilon_2\de... ...epsilon_3\delta_3)+\cdots+\delta_2f(x_{n-1}+\epsilon_n\delta_n)\end{displaymath}$

與區間 $\delta_i$ 及數量 $\epsilon_i$ 的選取有關。如果它具有如下的性質。無論 $\delta_i$ 與 $\epsilon_i$ 如何選取，當所有的 $\delta_i$ 變成無窮小時，它趨近於一個固定的極限值A則這個值稱為 $\int_a^bf(x)$ 。如果它沒有這個性質，則 $\int_a^bf(x)$ 是無意義的。

與Cauchy的積分定義作比較，Riemann的積分定義不僅僅是用區間[x_i-1,x_i]中的任一點 $\overline{x_i}$ 的函數值 $f(\overline{x_i})$ 來取代f(x_i-1)的技術性考量而已，更重要的一點是:Riemann並不強調函數f(x)須要在區間[a,b]上連續，於是，不連續函數（現代意義下）真正地進入了數學領域。按著，Riemann提出了一個問題:

讓我們決定這個概念正確的程度，在什麼情況下，函數是可積，在什麼情況下又不然。

也就是說，Riemann考慮他的可積函數可以涵蓋多少種函數?為此，Riemann從有界函數 f(x)開始:並像Cauchy一樣忽略了實數系的完備性，而直接寫下了下列函數可積的充要條件

$\begin{displaymath}R(1)\quad\lim_{\vert\vert P\vert\vert\rightarrow 0}(D_1\delta_1+D_2\delta_2+\cdots+D_n\delta_n)\end{displaymath}$

其中 $\delta_i=x_i+x_{i-1}$ 是由區間[a,b]的分割P所形成的第i個子區間的長度; ||P||就是所謂分割P的範數，也就是所有也的最大值;而D_i為f(x)在第i個子區間[x_i-1,x_i]上的最大值與最小值的差。

Riemann按著給出可積函數的另一個判斷條件。給定 $\sigma>0$ ，及區間[a,b]的分割 P,若 $S(\sigma,P)$ 表示振幅 $D_i>\sigma$ 的子區間的總長度。則定積分存在的充要條件為

$\begin{displaymath}R(2)\quad\lim_{\vert\vert P\vert\vert\rightarrow 0}S(\sigma,P)=0\end{displaymath}$

Riemann關於函數可積的兩個充要條件多少影響了往後積分理論的發展。首先，第一個條件多少有點像Camille Jordan以容積(content)的觀點寫下函數可積的充要條件

$\begin{displaymath}inf\Sigma_{i=1}^nM_ic(E_i)=sup\Sigma_{i=1}^nm_ic(E_i)\end{displaymath}$

其中 $[a,b]=E_i\bigcup E_2\bigcup\cdots\bigcup E_n$ , $E_i\bigcap E_i=\o$ ,m_i, M_i表示函數f(x)在點集E_i的最大下界與最小上界。而式中的inf,sup取盡所有可能區間[a,b]的分割E_i。從這裡才有可能把積分定義推廣到最大的範圍，然而， Riemann並沒有認識到這一點，最重要的是集合論還末發展起來，這只有待後人以另外一種方式改寫這些條件後，才能得到Riemann積分的擴展。但是，Rimann的積分定義已經是用Cauchy和的方式所能定義的積分的最廣形式了，這似乎是不能否認的。至於Riemann給出的第二個積分存在的充要條件;反映出積分的存在性僅與函數f(x)不連續點所構成的集合的結構有關，至於，函數f(x)在這些點的值是多少倒是沒有關係，這其實就相當於函數在零測集上改變函數值並不影響其積分值:而零測集的概念也是在Lebesgue積分發展中佔有重要的角色。我們還會在後文中回到這兩個Riemann積分存在的充要條件。

值得一提的是Riemann不願像Cauchy一樣斷定：連續函數都是可積的，因為，連續函數在閉區間上是均勻連續的嚴格證明一直到1870年代才得到。在這一點上，表現出Riemann 的風格與Cauchy不同。雖然，Cauchy寫作論文之快與多，甚至多到讓巴黎科學院因為無法應付快速增長的印刷費，而通過了一項規定：「禁止發表超過四頁的文章」，然而，Cauchy 也同樣遭到一些人對於Cauchy為文草率的嚴厲批評。然而，Riemann或許因為受到Guass 不輕易發表作品的影響，或許也是Riemann生命短暫的緣故，Riemann一生發表的作品很少，但是，每一件作品都在那個領域裡掀起了革命性的波濤。

雖然，Riemann並沒有證明：連續函數都是可積的，但是，Riemann在就職論文的最後，給出了不連續點集包含一個稠密集，但卻可積的函數。由於這個函數具有分析上的重要性，所以，我們按著介紹這個函數。設x為任一個不為 $\frac{1}{2}$ 奇數倍的實數，則 (x)=x-[x]，其中[x]為高斯函數;當x為 $\frac{1}{2}$ 的奇數倍時，則函數(x)=0 ，由此，Riemann的函數f(x)定義為下列無窮級數的和

$\begin{displaymath} f(x)=\frac{(x)}{1^2}+\frac{(2x)}{2^2}+\frac{(3x)}{3^2}+\cdots+\frac{(nx)}{n^2}+\cdots \end{displaymath}$

(18)

可以證明，f(x)的不連續點為型如 $\frac{m}{2n}$ 的數，其中m，n為互質的整數，而當 x為f(x)的不連續點時，其跳躍度為

$\begin{displaymath} f(x-0)-f(x+0)=\frac{1}{n^2}\sum_{p=1}^{\infty}\frac{1}{(2p+1)^2}=\frac{\pi^2}{8n^2} \end{displaymath}$

(19)

利用Riemann的第二個可積充要條件，很容易證明Riemann的函數f(x)是可積的。這個函數最重要的應該是其不連續點集有無窮多個且在直線上是稠密的，因為這表示出Riemann 允許具有無窮多個不連續點的函數進入其積分:而在Cauchy(或說Fourier)之前的積分函數則均是具有解析表示式的函數，Dirichlet的積分函數雖然放鬆一些，但是，Dirichlet 不允許他的積分函數有太多的不連續點（從拓樸的角度而言）。這個例子同時也說明了十八世紀數學家對於連續與可微的誤解：雖然，f(x)具有一個解析表示式，但是，它卻具有既多且密的不連續點；另一方面：它的連續點幾乎佈滿了整條直線，但是，它的不可微點也很多，這與我們現在對於連續函數的直觀了解有很大的出入。

Riemann有了更廣義的積分與函數的觀念之後，Riemann提出他用以研究三角級數的重要函數，設

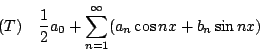
$\begin{displaymath}(T)\quad\frac{1}{2}a_0+\sum_{n=1}^{\infty}(a_n\cos nx+b_n\sin nx)\end{displaymath}$

為一滿足當 $n\rightarrow 0$ ，a_n, $b_n\rightarrow 0$ 三角級數，把(T)形式上連續積分兩次，得到了著名的Riemann函數

$\begin{displaymath} F(x)=\frac{1}{4}a_0x^2+\alpha x+\beta-\sum_{n=1}^{\infty}\frac{1}{n^2}(a_n\cos nx+b_n\sin nx) \end{displaymath}$

(20)

其中α，β為積分常數。我們無法在此深入一些細節，在這裡僅指出Riemann 從這個函數出發：得出一個函數是否可以表示為Fourier級數的充要條件。更重要的是， Riemann提出了一個深刻的問題：給定一個函數，它的三角級數表示式是否唯一？由於這個問題，使得 Georg Cantor（1845～1918）開創了集合論這個劃時代的研究。

　1│2│3│4│5│6　


	（若有指正、疑問……，可以在此留言或寫信給我們。）

EpisteMath (c) 2000 中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有

編輯：黃信元

最後修改日期：4/26/2002