| |
對自然的深入研究是數學發現最重要的源泉。
──Jean Baptiste Joseph Fourier
本節標題的這段話是Fourier(1768∼1830)最常被引用的一段話。它同時也暗示著 Fourier 是一位數學物理學家。Fourier 於1768年出生於一個貧窮的裁縫師的家裡,九歲時,雙親就相繼去逝:由教會送去軍校
就讀,畢業後,由於出身是裁縫師兒子的緣故,因此 Fourier 無法獲
得軍銜。比 Fourier 於是想到巴黎繼續他的數學研究:可是由於法國大
革命爆發:因此,Fourier 回老家教幾年書。法國大革命爆發後,由於
Fourier 對因恐怖活動而遭受害的人的辯護,而被捕入獄。出獄後,進
入巴黎師範學院念書,雖然為期不久,但是,也顯現出他在數學方面
的才能,或許是這樣的原因,當1795年,巴黎綜合工科學校成立時,他
立即被選為 J.L. Lagrange(1736∼1813)以及 G. Monge(1746∼1818)這兩位
當代法國的數學大師的助教,但是,不久(1798年)即與 Monge 跟隨拿破崙至埃及遠征。在埃及期間,Fourier 就對熱傳導問題產生極大的興趣,據說,他在埃及的熱學實驗以及研究工作顯示:沙漠地區的熱對於人體的健康有很大的幫助,因此,他經常穿著溼的衣服。並將自己包裹的像木乃伊一樣,住在溫度高到令人難以忍受的房間裡,或許是他對熱太酷愛了,以致於當他去逝時,身上仍熱得像剛煮過一樣。但是,Fourier 的主要研究成果卻是在1801年這一年有了轉變,在這一年,法國於特拉法加戰役中敗給英國,Monge 隨拿破崙倉促地回到法國,稍後,Fourier 也回到法國。回國之後,起先,Fourier 是希望能獲取教職,但是,由於拿破崙賞識他的行政能力,於是:他被任命為伊澤爾地區的首府格勒諾布爾的官員,就在這裡,Fourier 開始了熱傳導問題的主要研究及實驗。
Fourier 的主要研究成果發表於他向巴黎科學院所提交的兩篇論文。第一篇是於1807年向巴黎科學院提交的:標題為〈熱的傳播〉(Mémoire sur la propagation de la chaleur),主要是處理一些諸如矩形、環狀、球形、柱形等特殊形狀連續體的熱傳導問題:論文的審查人為法國著名的三 L 數學家:Laplace、Legendre以及 Lagrange,其中,Lagrange 持著相當反對的態度,原因是 Fourier 於論述過程中,表示出下列令人訝異的論斷:Fourier 認為不論定義在 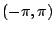 上的函數 f(x) 是如何任意,它一定可以用一個無窮三角級數表示出來:也就是說,存在適當的實數 an,bn 使得下式成立 上的函數 f(x) 是如何任意,它一定可以用一個無窮三角級數表示出來:也就是說,存在適當的實數 an,bn 使得下式成立
這個論證恰與 Lagrange 在十八世紀末關於弦振動問題的研究結果相矛盾,話雖如此:但是,由於 Fourier 的研究內容是如此的富有創意,這些數學家們還是於回信時,鼓勵他繼續將其內容嚴密化,科學院並在1810年懸賞徵求關於熱傳導的問題。
Fourier 經過四年的努力,於1812年再度向巴黎科學院提交一篇論文:標題為〈熱在固體中的運動理論〉(Theorie du mouvement de chaleur clansles corps solides),內文不僅修正了1807年論文的部份內容,也增加了關於無窮大物體的熱傳導分析。再一次地:由三 L 負責評審,他們給予的評審意見是:「Fourier 的論文思想新穎,給出了解決熱傳導等問題的重要方法,有很高的實用價值。同意發給高額獎金」。因此,Fourier 在這次的徵文中,獲得了懸賞的巨額獎金:但是,也因為 Lagrange 相當堅持該篇論文的嚴密性緣故,而無法在科學院的「研究報告」(Memoires) 上發表。
Fourier 對於巴黎科學院無法接受他的論文感到很生氣,不過,他還是繼續他的工作,並於1822年發表他關於熱傳導的重要數學著作《熱的解析理論》(Théorie analytique de la chaleur),並於發表該書的兩年後,當上曾令他生厭的巴黎科學院的祕書,並一直到終老。然而也由於職務之使,才使他得以將他的論文一字不改地發表於「研究報告」(Memoires) 上。
接下來,我們要了解一下 Fourier 在1807年的論文所考慮的一個問題:求區域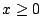 , ,
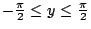 中,當物體呈現穩定狀態時,其溫度函數 T(x,y) 為何?也就是底下的偏微分方程式 中,當物體呈現穩定狀態時,其溫度函數 T(x,y) 為何?也就是底下的偏微分方程式
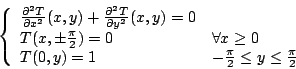 |
(7) |
其中區域底邊上的溫度恆為 1。Fourier 首先利用所謂的分離係數法得
到(7)式的一族基本解
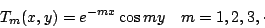 |
(8) |
由於溫度函數 T(x,y) 在
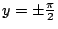 時均等於 0,於是 m 只能取值 時均等於 0,於是 m 只能取值 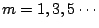 , 再由溫度函數 T(x,y) 在底邊 x=0 時,恆為 1,就可得到下列的方程式 , 再由溫度函數 T(x,y) 在底邊 x=0 時,恆為 1,就可得到下列的方程式
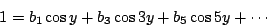 |
(9) |
Fourier 認為(9)式的右邊為 y 的函數,稍後,他注意到
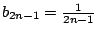 , ,
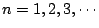 ,於是,(7)式的一般解為 ,於是,(7)式的一般解為
Fourier 接下來考慮:若底邊
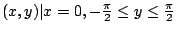 的溫度不是 1,而是一般的函數 的溫度不是 1,而是一般的函數 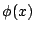 則溫度分佈函數 T(x,y) 又如何?也就是說:如何找出參數 b1,b2,b3, ...。為此,Fourier 首先考慮 則溫度分佈函數 T(x,y) 又如何?也就是說:如何找出參數 b1,b2,b3, ...。為此,Fourier 首先考慮 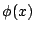 是奇函數的情形,也就是如何求解下列無窮級數的係數 bn: 是奇函數的情形,也就是如何求解下列無窮級數的係數 bn:
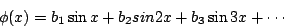 |
(10) |
這個問題相當於是 Fourier 前人所遭遇的問題,也就是對於任意函數 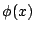 是否可以展開成為一無窮三角級數和。Fourier 起先是分別將 是否可以展開成為一無窮三角級數和。Fourier 起先是分別將 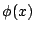 , ,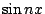 展開成在 x=0 附近的 MacLaurin 級數,然後代入(10)式比較係數,再經過一些複雜、且帶有古怪的作法,可以得到 展開成在 x=0 附近的 MacLaurin 級數,然後代入(10)式比較係數,再經過一些複雜、且帶有古怪的作法,可以得到
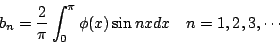 |
(11) |
Fourier 作完這項計算複雜的大工程之後,Fourier 指出:bn 也可以依如下的程序而得到。首先將(10)兩邊同乘以 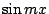 並將兩邊同時從 0 到 π 作積分,得到 並將兩邊同時從 0 到 π 作積分,得到
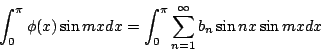 |
(12) |
將(12)式的右邊積分運算與求和運算交換。亦即作逐項積分就可得到 bn。接下來當然是考慮 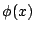 是偶函數的情形,再其次是一般函數的情形。總結他說:若函數是以 是偶函數的情形,再其次是一般函數的情形。總結他說:若函數是以 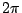 為週期的函數,則 f(x) 可以展開為如下的三角級數 為週期的函數,則 f(x) 可以展開為如下的三角級數
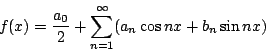 |
(13) |
其中
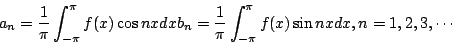 |
(14) |
這項結論其實 Fourier 的前輩們早已取得,那麼,Fourier 的特點在哪裡呢?Fourier 將定積分
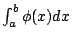 解釋為 解釋為 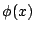 與 x=a,x=b;以及 x 軸所圍成區域的面積,於是 與 x=a,x=b;以及 x 軸所圍成區域的面積,於是 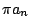 的意義就是 的意義就是
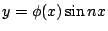 曲線下的面積。這對於我們而言:似乎是再明顯也不過了,但是回想中學時代所教授的積分概念,雖然老師也指出求定積分就相當於求某區域面積的事實,但是,大部分的時間,都將求定積分轉為求原函數,也就是相當於求一函數 g(x),使得 曲線下的面積。這對於我們而言:似乎是再明顯也不過了,但是回想中學時代所教授的積分概念,雖然老師也指出求定積分就相當於求某區域面積的事實,但是,大部分的時間,都將求定積分轉為求原函數,也就是相當於求一函數 g(x),使得
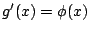 成立,而非利用求和的觀念來求定積分。令人驚訝的是十八世紀以及十九世紀初的數學家都有著相同的態度,即使有人認為求積分就是相當於求面積,但也不是主流。因此,若堅持求函數 成立,而非利用求和的觀念來求定積分。令人驚訝的是十八世紀以及十九世紀初的數學家都有著相同的態度,即使有人認為求積分就是相當於求面積,但也不是主流。因此,若堅持求函數 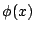 定積分是求其所對應的原函數,那麼 定積分是求其所對應的原函數,那麼
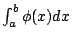 的存在性就得基於 的存在性就得基於 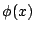 必滿足十八世紀數學家意義下的連續(也就是有解析表示式):而且可由「反微分」計算出來。這麼多的要求,當然也就使得 必滿足十八世紀數學家意義下的連續(也就是有解析表示式):而且可由「反微分」計算出來。這麼多的要求,當然也就使得
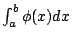 的存在性極為可議了!由於 Fourier 這種對積分的觀點,因此,他認為對於任意函數(不論是 d'Alembert、Euler 或是任何意義下的函數) 的存在性極為可議了!由於 Fourier 這種對積分的觀點,因此,他認為對於任意函數(不論是 d'Alembert、Euler 或是任何意義下的函數)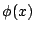 而言, 而言,
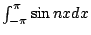 均是有意義的,所以, 均是有意義的,所以,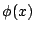 均可透過計算 均可透過計算
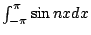 , ,
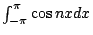 ,從而得到任意函數 ,從而得到任意函數 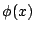 三角級數表示法。 三角級數表示法。
正因為如此,當 Lagrange 發現 Fourier 法提出有力的數學證明時,當然遭到Lagrange的反駁,至少 Lagrange 在十八世紀末那場振動的論戰中,是站在Euler的立場並反對 Daniel 三角級數的觀點。然而,Fourier 並不因此而退縮了,他採取「實驗」的手段,選取了大量的函數,計算每個函數的前面幾個 an,bn 並將所得的三角級數前幾項所構成的函數圖形與原來函數圖形作比較,因而,更肯定自己的結論,並且了以下的結論:「不管函數 f(x) 在區間
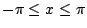 外如何,由(14)式的 an,bn 所形成的三角級數(13)恆可以表示 f(x),這就是為什麼早期的數學家不能接受任何一個函數可展開為三角級數的原因,正是他們沒有能夠看到兩個函數可以在一給定的區間上相合,但不一定在此區間外相合,在給定的條件下,級數真正確定的是函數在 外如何,由(14)式的 an,bn 所形成的三角級數(13)恆可以表示 f(x),這就是為什麼早期的數學家不能接受任何一個函數可展開為三角級數的原因,正是他們沒有能夠看到兩個函數可以在一給定的區間上相合,但不一定在此區間外相合,在給定的條件下,級數真正確定的是函數在 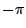 到 π 區間上的值,在區間外則週期地重覆著」。在這裡,我們多少可以看到純數學家與數學物理學家的不同,Lagrange 以其作品的嚴密性著稱,而 Fourier 卻寧可相信他的物理直觀。 到 π 區間上的值,在區間外則週期地重覆著」。在這裡,我們多少可以看到純數學家與數學物理學家的不同,Lagrange 以其作品的嚴密性著稱,而 Fourier 卻寧可相信他的物理直觀。
Fourier 的「錯誤」結論使人聯想到:如果任意函數都可以用三角級數表示出來,那麼連續與不連續函數(在十八世紀的意義下)又有什麼差別呢?這個問題就導引著往後的數學家對分析的基礎前進。Fourier 所引發的另外的一個問題是三角級數是否收斂,以及可否逐項積分?這些問題在當時看來是理所當然成立,因為甚至收斂性的問題,當時的數學家都未曾認真考慮過:更不必說逐項積分。但是,在往後的幾節裡,我們將看到這些問題卻是激起集合論誕生的重要問題。
|
|
|