Green 定理與應用 (第 7 頁)

　1│2│3│4│5│6│7　

Green 定理與應用（第 7 頁）

林琦焜

首頁 | 搜尋

．原載於數學傳播第二十一卷第四期
．作者當時任教於成功大學數學研究所
‧對外搜尋關鍵字

七、Green 定理在複變函數論之應用

應用一：

Cauchy 定理： ${\mathcal{R}}$ 為複數平面上之單連通區域 (simply connected domain)，f 為定義在 ${\mathcal{R}}$ 上之單值 (single value) 連續可微且解析的函數，則

$\begin{displaymath} \oint_C f(z) dz =0 \eqno {(42)} \end{displaymath}$

其中 C 為包含在 ${\mathcal{R}}$ 內之任意分段平滑之 Jordan 曲線。

解：假設 f=u+iv , z=x+iy 則複變積分（實際上就是線積分）為

$\begin{eqnarray*} \oint_C f(z)dz &=& \oint_C (u+iv)d(x+iy) \\ &=& \oint_C udx -vdy + i \oint_C vdx + udy \end{eqnarray*}$

但 f 可微且

$\begin{eqnarray*} f'(z) &=& \frac{\partial u}{\partial x} + i \frac{\partial v}{... ... \frac{\partial v}{\partial x} - i \frac{\partial u}{\partial y} \end{eqnarray*}$

因為 u,v 之偏導數為連續，因此可利用 Green 定理分別作用到實部與虛部得

$\begin{eqnarray*} \oint_C (udx -vdy) &=& \int \!\! \int_{\mathcal{R}}(-\frac{\pa... ...ac{\partial u}{\partial x} - \frac{\partial v}{\partial y})dxdy \end{eqnarray*}$

由 Cauchy-Riemann 方程（f 為解析函數）

$\begin{displaymath} \frac{\partial u}{\partial x}=\frac{\partial v}{\partial y},... ...rac{\partial u}{\partial y}= - \frac{\partial v}{\partial x} . \end{displaymath}$

知上面兩個積分為零，故可結論

$\begin{displaymath} \oint_C f(z)dz =0 . \end{displaymath}$

複變積分的物理意義可由第三節的討論而得，仿 Cauchy 定理之證明；

$\begin{eqnarray*} \oint_C \overline{f}(z)dz &=&\oint_C (u-iv)d(x+iy)\\ &=&\oint... ...eries{m}\selectfont \char 190} (flux)} \qquad\qquad \eqno{(43)} \end{eqnarray*}$

當然可以利用 Green 定理將之化為二重積分，（比較(9)，(16)）

$\begin{eqnarray*} \oint_C \overline{f}(z) dz &=&\int \!\! \int_{\mathcal{R}} (\... ...a \cdot F )dA \qquad\qquad\qquad\qquad \eqno{(44)} && (F=(u,v)) \end{eqnarray*}$

f 之複變積分轉化為向量場 F=(u,v) 之旋度與散度的二重積分，換句話說，透過對向量場 F=(u,v) 的旋度與散度的研究可幫助我們對函數 $\overline{f}$ 或 f 的認識，實際上 Cauchy-Riemann 方程就是散度與旋度的組合：

$\begin{displaymath} \left\{ \begin{array}{ll} u_x = (-v)_y \\ u_y = -(-v)_x \en... ... \mbox{curl} F = v_x - u_y = 0 \end{array}\right. \eqno{(45)} \end{displaymath}$

在近代分析中極負盛名的補償緊緻法 (comnpensated compactness method) 之精神便是，如果向量場之散度與旋度有很好的性質，則原向量場可以得到更好的緊緻性（就是所謂的散度旋度引理 (div-curl lemma)）。

應用二：

(40)式可視為複數形式的 Green 定理；我們先看看座標變換： $(x,y)\longmapsto (z,\overline{z})$

$\begin{displaymath} \left\{ \begin{array}{l} z =x +iy \\ \overline{z} = x -iy... ...= \frac{1}{2i}(z-\overline{z}) \end{array}\right. \eqno{(46)} \end{displaymath}$

由全微分或連鎖律 (chain rule) 可得

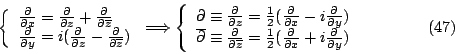
$\begin{displaymath} \left\{ \begin{array}{l} \frac{\partial}{\partial x} = \frac... ...i \frac{\partial}{\partial y} ) \end{array}\right. \eqno{(47)} \end{displaymath}$

因此Laplace 算子可表為

$\begin{displaymath} \nabla = \partial_{xx} + \partial_{yy} = 4 \partial \overline{\partial} = 4 \overline{\partial} \partial \end{displaymath}$

現在考慮可微分函數 (differentiable function)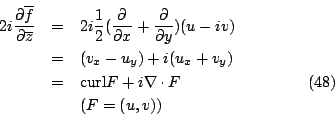， $\overline{f}=u-iv$ ，則

$\begin{eqnarray*} 2i \frac{\partial \overline{f}}{\partial \overline{z}}&=& 2i\f... ... \cdot F \qquad\qquad\qquad\qquad \eqno{(48)} \\ && (F=(u,v)) \end{eqnarray*}$

另一方面利用微分型式 (differential form) 之公式可得

$\begin{eqnarray*} d[fdz]&=&\frac{\partial f}{\partial z} dz \wedge dz + \frac{\p... ...rline{z}} dxdy \qquad\qquad\qquad\qquad\qquad\qquad \eqno{(49)} \end{eqnarray*}$

複數形式的 Green 定理： $f=f(z,\overline{z})$ 為連續且其偏導數亦為連續則

$\begin{displaymath} \oint_C \overline{f}(z)dz = 2i \int \!\! \int_{\mathcal{R}} ... ...{f}}{\partial\overline{z}} d\overline{z} \wedge dz \eqno{(50)} \end{displaymath}$

$\begin{displaymath} \oint_C f(z)dz = 2i \int \!\! \int_{\mathcal{R}} \frac{\part... ...l f}{\partial\overline{z}} d\overline{z} \wedge dz \eqno{(51)} \end{displaymath}$

其中 $C=\partial \mathcal{R}$ ， $\mathcal{R}$ 滿足 Green 定理之要求。

如果 f 為解析函數 (analytic function) 則

$\begin{displaymath} 2i \frac{\partial f}{\partial \overline{z}} =(-v_x - u_y) + i(u_x - v_y) = 0 \end{displaymath}$

分別取實部與虛部等於零，這就是著名的 Cauchy-Riemann 方程式：

$\begin{displaymath} u_x = v_y \qquad u_y = -v_x \eqno{(52)} \end{displaymath}$

再一次得到 Cauchy 定理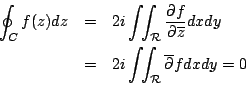

$\begin{eqnarray*} \oint_C f(z)dz &=& 2 i \int \!\! \int_{\mathcal{R}} \frac{\par... ...=& 2 i \int \!\! \int_{\mathcal{R}} \overline{\partial}fdx dy =0 \end{eqnarray*}$

因此我們可以說 Green 定理的推廣就是 Cauchy 定理的推廣。

應用三：

Cauchy 積分公式：假設 $f \in C^1(\overline{{\mathcal{R}}})$ ，則

$\begin{displaymath} f(\xi) =\frac{1}{2 \pi i}\int_{\partial {\mathcal{R}}} \frac... ...e{z}} \frac{1}{z - \xi} dz \wedge d \overline{z} \eqno{(53)} \end{displaymath}$

這個公式顯然是在一般大學部複變函數理論之 Cauchy 積分公式之推廣。

證明：我們仿前面之例題3計算線積分之方法考慮區域

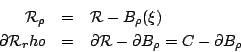
$\begin{eqnarray*} {\mathcal{R}}_\rho &=& {\mathcal{R}} - B_\rho (\xi) \\ \parti... ...& \partial {\mathcal{R}} - \partial B_\rho = C - \partial B_\rho \end{eqnarray*}$

並且取函數

$\begin{eqnarray*} & & F(z)= \frac{f(z)}{z- \xi} \\ & \Longrightarrow & \frac{\p... ...e{z}} = \frac{\partial f}{\partial \overline{z}}\frac{1}{z- \xi} \end{eqnarray*}$

則由 Green 定理(50)知

$\begin{displaymath} \oint_{\partial {\mathcal{R}}_\rho} F(z)dz = \int \!\! \int_... ...ac{\partial F}{\partial \overline{z}} d \overline{z} \wedge dz \end{displaymath}$

因此

$\begin{displaymath} \oint_C \frac{f(z)}{z- \xi}dz - \oint_{\partial {\mathcal{B}... ...ine{z}} \frac{1}{z- \xi} d \overline{z} \wedge dz \eqno{(54)} \end{displaymath}$

令 $\rho \rightarrow 0$ 且由連續性之特性可得

$\begin{displaymath} \oint_{\partial B_\rho} \frac{f(z)}{z-\xi} dz \rightarrow 2 \pi i f(\xi) \eqno{(55)} \end{displaymath}$

另一方面由極座標知

$\begin{displaymath} d \overline{z} \wedge dz = 2i dxdy = 2irdrd \theta \end{displaymath}$

$\begin{displaymath} \frac{1}{\vert z-\xi\vert}d \overline{z} \wedge dz = 2idrd \theta \eqno{(56)} \end{displaymath}$

所以(55)成為 Cauchy 積分公式（令 $\rho \rightarrow 0$ ）

$\begin{displaymath} f(\xi)=\frac{1}{2 \pi i} \oint_{C} \frac{f(z)}{z-\xi} dz + ... ...ial \overline{z}} \frac{1}{z - \xi} dz \wedge d \overline{z} \end{displaymath}$

註 1：Cauchy 積分公式是個古老且優美的結果，通常我們極容易就認定，這就是其終極形式，然而這個「神話」卻於1978年代由 Kerzman 與 Stein 在研究多複變函數 (Several Complex Variables) 所打破，這個結果，我們稱為 Kerzman-Stein 公式，有興趣之讀者可參閱相關資料。

註 2：如果 f 為解析函數 (analytic function)， $\frac{\partial f}{\partial \overline{z}}=0$ ，則該公式就回到傳統的 Cauchy 積分公式，它告訴我們，對 $\mathcal{R}$ 內任一點 $\xi \in \Omega$ ，函數值 $f(\xi)$ ，可由表為邊界 $C=\partial \mathcal{R}$ 之路徑積分，而這個表現定理 (representation theorem) 也提供了 Cauchy-Riemann 方程 $\frac{\partial f}{\partial \overline{z}}=0$ 解的公式。

應用四：

如果考慮微分方程（ $\overline{\partial}$ 問題）

$\begin{displaymath} \frac{\partial f}{\partial \overline{z}}=h \eqno{(57)} \end{displaymath}$

Cauchy 積分公式(53)告訴我們右邊第一式可視為齊次解 (homogeneous solution)，因此 Cauchy 積分公式(53)同時提議 $\overline{\partial}$ 問題(58)之解為

$\begin{displaymath} f(\xi) = \frac{1}{2 \pi i}\int_{\partial {\mathcal{R}}} \fra... ...hcal{R}}\frac{h}{z- \xi} dz \wedge d \overline{z} \eqno{(58)} \end{displaymath}$

$\overline{\partial}$ -問題：假設 $f \in C^\infty (\overline{\mathcal{R}})$ ，則非齊次 Cauchy-Rieman 微分方程

$\begin{displaymath} \frac{\partial u}{\partial \overline{z}}=f(z,\overline{z}) \end{displaymath}$

之解可表為

$\begin{displaymath} u(\xi) = v(\xi) + \frac{1}{2 \pi i} \int \!\! \int_{\mathcal... ...(z,\overline{z})}{\xi-z} dz \wedge d \overline{z} \eqno{(59)} \end{displaymath}$

$v(\xi)$ 為任意的解析函數 (analytic function)

解：這問題是解決可由複變函數之理論而來，但我們比較喜歡用偏微分方程的技巧，由 Cauchy 積分方式，直觀而言，我們需要處理的是

$\begin{displaymath} \frac{\partial }{\partial \overline{z}} \frac{1}{z-z_0}= ? \end{displaymath}$

顯然可知

$\begin{displaymath} \frac{\partial }{\partial \overline{z}}\frac{1}{z-z_0}=0 \qquad \forall z \neq z_0 \end{displaymath}$

因此我們可以假設

$\begin{displaymath} \frac{\partial}{\partial \overline{z}} \frac{1}{z-z_0} = c \... ...elta(\overline{z}-\overline{z}_0) =c\delta(x-x_0)\delta(y-y_0) \end{displaymath}$

c 為一待求之常數，不失一般性可 z₀=0 則

$\begin{displaymath} \frac{1}{z}=\lim_{\varepsilon \rightarrow 0} \frac{\overline{z}}{z\overline{z}+\varepsilon^2} , \qquad \varepsilon >0 \end{displaymath}$

直接微分得

$\begin{displaymath} \frac{\partial}{\partial \overline{z}} (\frac{\overline{z}}... ...^2)^2} =\frac{\varepsilon^2}{(\vert z\vert^2+\varepsilon^2)^2} \end{displaymath}$

因此

$\begin{eqnarray*} c&=&\int \!\! \int_{\mathcal{R}^2} \frac{\partial }{\partial \... ... 0} 2 \pi i \int_0^\infty \frac{2rdr}{(r^2+1)^2} \\ &=& 2 \pi i \end{eqnarray*}$

換句話說

$\begin{displaymath} \frac{\partial}{\partial \overline{z}} \frac{1}{z-z_0} = 2\pi i \delta (z-z_0) \delta(\overline{z}-\overline{z}_0) \end{displaymath}$

所以 $\frac{1}{2 \pi i} \frac{1}{z-z_0}$ 故一基本解 (fundamental solution) 故 $\overline{\partial}$ 問題之解為

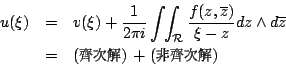
$\begin{eqnarray*} u(\xi) &=& v(\xi) + \frac{1}{2 \pi i} \int \!\! \int_{\mathcal... ...nus0.1pt{\fontfamily{cwM2}\fontseries{m}\selectfont \char 106})} \end{eqnarray*}$

應用五：

在複變函數論的發展歷史中，是與流體力學有非常密切之關係，特別是二維穩定、不可壓縮、無旋度、不具黏性的流體 (steady two-dimensional flow of an incompressible, irrotational, inviscid fluid) 其中最著名的是 Bernoulli 定律，這定律說明了飛機飛行的原理，是航空史第一個最重要的定律：

Bernoulli 定律：

$\begin{displaymath} \begin{array}[t]{c} P+ \frac{1}{2}\rho\vert w\vert^2 = \mbox... ...}\fontseries{m}\selectfont \char 98})} \end{array} \eqno{(60)} \end{displaymath}$

假設 Ω 為 xy-平面上的一個單連通區域 (simply connected domain) 而曲線

$\begin{displaymath} C = \{ z = z(s) = x(s)+iy(s), \; 0 \leq s \leq L \} \end{displaymath}$

則代表 Ω 中一條有長度分段平滑的封閉區線，因此曲線 C 上任一點之單位切向量與單位朝外法向量為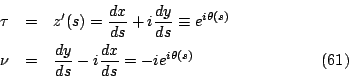

$\begin{eqnarray*} \tau &=& z'(s)= \frac{dx}{ds} + i \frac{dy}{ds}\equiv e^{i \th... ...{ds} = - ie^{i \theta(s)} \qquad\qquad\qquad\qquad \eqno{(61)} \end{eqnarray*}$

另外假設流體的速度為

$\begin{displaymath} w=u+iv \eqno{(62)} \end{displaymath}$

則由(43)式可知

$\begin{eqnarray*} \oint_C \overline{w}dz &=&\oint_C udx + vdy + i\oint_C - vdx ... ...electfont \char 34} (expansion)} \qquad\qquad\qquad \eqno{(63)} \end{eqnarray*}$

實部表示沿曲線 C 之環流，虛部則表示曲線內面積之變化率，由於我們所考慮的是特殊的流體（穩定、不可壓縮、無旋度、不具黏度性）這個假設告訴我們在曲線 C 內唯一作用到流體的力是流體本身的壓力（法向量方向）必須等於通過 C 之動量通量 (momentum flux)，因此

$\begin{displaymath} \int_C [P \nu + \rho w(w\cdot v)]ds =0 \eqno{(64)} \end{displaymath}$

ρ 表示流體之密度，P 為其壓力，利用關係式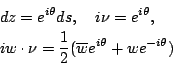

$\begin{eqnarray*} && dz = e^{i \theta}ds, \quad i \nu = e^{i \theta}, \\ && iw \cdot \nu = \frac{1}{2}(\overline{w}e^{i \theta} + w e^{-i \theta}) \end{eqnarray*}$

可以將(65)改寫為

$\begin{displaymath} \oint_C(P+\frac{1}{2}\rho\vert w\vert^2)dz + \frac{1}{2}\oint_C \rho w^2 d \overline{z}= 0 \eqno{(65)} \end{displaymath}$

最後我們假設流體是均勻的 (homogeneous) 因此 $\rho =$ 常數，因為 $\overline{w}$ 是解析函數，所以 $\overline{w}^2$ 也是解析函數，故由 Cauchy 定理可知

$\begin{displaymath} \int_C \overline{w}^2 dz = 0 \quad \Rightarrow \quad \int_C w^2 d \overline{z}=0 \end{displaymath}$

所以(66)式化簡為

$\begin{displaymath} \oint_C (P+\frac{1}{2} \rho \vert w\vert^2) dz= 0 \eqno{(66)} \end{displaymath}$

由 Morera 定理可結論被積分函數 $P+ \frac{1}{2} \rho \vert w\vert^2$ 為解析函數，但由 Green 定理(51)式，可知唯一可能的實值解析函數 (real-valued analytic function) 是常數函數，因此可結論

$\begin{displaymath} P+\frac{1}{2}\rho\vert w\vert^2 =\mbox{{\fontfamily{cwM1}\fo... ...us0.1pt{\fontfamily{cwM1}\fontseries{m}\selectfont \char 98}}. \end{displaymath}$

: 1. 數學之內容方法及意義(I, II, III)；徐氏基金會出版(1970)。
: 2. The Cauchy Transform, Potential Theory and Conformal Mapping; Steven R. Bell; CRC PRESS (1992).
: 3. Introduction to Calculus and Analysis (I, II); R. Courant and F. John; Springer-Verlag (1989).
: 4. Complex Variables; G. Polya and G. Latta; John Wiley and Sons, Inc. (1974).
: 5. Vector and Tensor Analysis; 2nd ed., E.C. Young; Marcel Dekker, Inc. (1993).

　1│2│3│4│5│6│7　


	（若有指正、疑問……，可以在此留言或寫信給我們。）

EpisteMath (c) 2000 中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有

編輯：朱安強 ∕ 繪圖：簡立欣

最後修改日期：4/26/2002