由於曲線 C 的變化可大可小一般而言並沒有明顯的參數式,因此無法直接求線積分,然而我們可利用逼近 (approximation) 的概念來處理,這正是數學尤其是分析 (analysis) 的主要技巧。
長方形
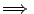 多邊形 多邊形
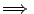 
I.  為一長方形 為一長方形
 之邊界
C = C1 + C2 + C3 + C4 之邊界
C = C1 + C2 + C3 + C4
因此利用微積分基本定理可得
II. 假設  可表為 可表為
我們分別處理
P(x,y) , Q(x,y)
同理可得
兩者合併
這就是 Green 定理,提供了我們關於線積分與面積分之關係,但這個逼近方法有個限制就是曲線 C 必須是有長度曲線 (rectifiable curve),而且還要用到一致收斂 (uniformly convergent) 的概念。對於更一般的區域 Green 定理仍然是對的,但已經超過微積分的範圍,讀者有興趣可參考微分幾何方面的書。
- 例題 1:
利用 Green 定理計算線積分
其中曲線 C 是由拋物線 y=x2 與直線 y=x 所圍區域之邊界。
解:要直接計算線積分勢必要將 C 化為參數式,然而利用 Green 定理取
則
因此
Green 定理說明一封閉曲線 C 之線積分與 C 所圍區域之面積分(雙重積分)之關係,因此在特殊情形之下,線積分之幾何意義為「面積」;例如取
則由 Green 定理知
通常可取 P,Q 如下:
- 系:
區域
 由分段平滑的封閉曲線 C 所圍成,其面積為: 由分段平滑的封閉曲線 C 所圍成,其面積為:
- 例題2:
試求橢圓
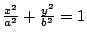 之面積。 之面積。
解:將橢圓表為參數式
利用系之結果得
為著更深入討論 Green 定理,我們再計算一個例題並從其中得到靈感。
- 例題 3:
已知 C 為任意封閉平滑曲線,試求線積分
解:首先假設 (0,0) 並不包含在 C 之內部,則
因此由 Green 定理知
其次,若 (0,0) 在 C 之內部,此時 (0,0) 為一奇異點 (singularity),克服這點的方法就是「避開它」,作一個半徑為 ρ,以 (0,0) 為圓心的圓 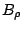 考慮區域 考慮區域
由於  並不包含 (0,0),因此利用前面的推論; 並不包含 (0,0),因此利用前面的推論;
但
 ,故 ,故
註 1:此處積分值為 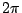 表示曲線 C 繞了奇異點 (0,0) 一圈,而積分值等於 0 則是沒有繞到 (0,0),這所對應的便是複變函數理論的繞數 (winding number),在流體力學則是環流 (circulation)。 表示曲線 C 繞了奇異點 (0,0) 一圈,而積分值等於 0 則是沒有繞到 (0,0),這所對應的便是複變函數理論的繞數 (winding number),在流體力學則是環流 (circulation)。
註 2:證明的過程中我們發現沿著曲線 C 之線積分等於沿著圓周
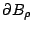 之線積分,這裡面的數學本質就是同倫理論 (homotopy theory),因此 Green 定理可推廣到單連通區域 (simply connected region),而這正是複變函數論研究的一重要主題,同時也說明複雜的曲線之線積分可化為簡單的曲線之線積分(例如圓周的線積分),這就是數學的精神──將複雜的問題化為簡單的問題。 之線積分,這裡面的數學本質就是同倫理論 (homotopy theory),因此 Green 定理可推廣到單連通區域 (simply connected region),而這正是複變函數論研究的一重要主題,同時也說明複雜的曲線之線積分可化為簡單的曲線之線積分(例如圓周的線積分),這就是數學的精神──將複雜的問題化為簡單的問題。
註 3:若 C1,C2 為任二條不相交的分段平滑封閉曲線而且都繞過原點 (0,0),則
這除了同倫理論之外,直接的意義就是該線積分對於形變 (deformation) 是一不變量。另外我們可透過極座標 (polar coordinate) 來看;令
則被積分函數 (integrand) 成為
因此這個線積分實際上就是在測量沿著曲線 C(逆時針方向)角度之變化量,當然若是繞了一圈則其變化量為 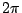 ,若是順時針方向繞了一圈則其變化量為 ,若是順時針方向繞了一圈則其變化量為 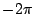 ,這個概念就是前面所說的繞數 (winding number)。 ,這個概念就是前面所說的繞數 (winding number)。
|
![\begin{eqnarray*}
& &\oint_C[P(x,y) \cos(\nu,x) + Q(x,y) \cos (\nu,y)]ds \\
&=&...
...=&\oint_C F \cdot \nu ds , \; v=(\frac{dy}{ds},- \frac{dx}{ds})
\end{eqnarray*}](img57.gif)