由(9)與(16)兩式,我們自然而然引進向量的概念:
另外向量場 F 的旋度 (curl) 為
散度 (divergence) 則為
所以 Green 定理((9),(16))可改寫為
分別表示切向量與法向量形式的 Green 定理,而其物理則分別是「功」(work) 與「通量」(flux),(20),(21) 兩式可推廣至更高維數空間,就是通稱的 Stokes 定理與散度定理 (Divergence Theorem)。
為何 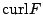 , ,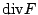 會被稱為旋度與散度呢?我們考慮特殊的區域 會被稱為旋度與散度呢?我們考慮特殊的區域 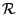 是以 (x0,y0) 為圓心,半徑是 r 的圓,則由連續性知 是以 (x0,y0) 為圓心,半徑是 r 的圓,則由連續性知
所以旋度是單位面積內之最大環流 (circulation),而散度則是單位面積內之通量(流量之變化),這個形式最大的好處不受座標的影響,如(18),(19)兩式,而且透過(22)式(即利用 Green 定理)我們可證明旋度和散度是與座標無關。
註 1:
如果
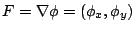 ,向量 (vector) F 為純量(scalar) ,向量 (vector) F 為純量(scalar) 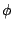 之梯度 (gradient) 則(21)式可改寫為 之梯度 (gradient) 則(21)式可改寫為
函數 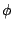 稱為位能函數 (potential function) 而 稱為位能函數 (potential function) 而
則是出名的 Laplace 算子,這是偏微分方程中最重要的算子。
註 2:
若取
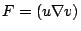 ,則由向量之計算得 ,則由向量之計算得
因此(21)式成為 Green 第一等式
若 u,v 互換,後兩式相減則可得 Green 第二等式
這些等式在偏微分方程中扮演著非常重要的角色。
註 3:
Green 定理的最好處理手法是利用微分形式 (differencial forms),我們簡單說明如下:線積分
之被積函數 (integrand) 為一階微分形式 (first order differential form)
L 之全微分 (total differential form) 為
因此 Green 定理可重新寫為微分形式 (differential form)
這個公式同時也說明在區域 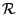 之積分及其邊界之積分兩者之關係,而實際上就是微積分基本定理之推廣,當然其精神則是──分部積分 (integration by part)。 之積分及其邊界之積分兩者之關係,而實際上就是微積分基本定理之推廣,當然其精神則是──分部積分 (integration by part)。
|