從醉月湖的面積談起 (第 3 頁)

　1│2│3│4│5│6│7　

從醉月湖的面積談起
向量微積分簡介（第 3 頁）

蔡聰明

首頁 | 搜尋

．原載於數學傳播第二十一卷第二期
．作者當時任教於台大數學系
‧對外搜尋關鍵字

3. 醉月湖的面積公式

公式(5)更是活生生的，它還可以再推廣，無窮化與連續化成平面上封閉曲線所圍成的領域（如醉月湖）之面積公式。為此，我們根據行列式的性質將(5)式稍作變形

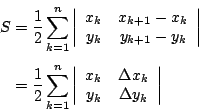$\begin{displaymath} \begin{eqalign} S &= {1\over 2} \sum\limits_{k=1}^n \left \v... ... x_k \\ y_k &\Delta y_k \end{array}\right \vert \end{eqalign}\end{displaymath}$

(6)

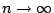如何連續化呢？由微積分我們知道，圓內接正 n 邊形的連續化（即 $n\rightarrow \infty$ ）就得到圓，差和分的連續化就是微積分，參見[3]。按此理，平面上封閉曲線 Γ 所圍成的領域，可以看作是邊長為無窮小 (infinitesimal) 的無窮多邊之多邊形（我們採無窮小論證之觀點）。所謂「連續化」在作法上就是將

和分 Σ 改為積分 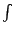$\int$
差分 Δ 改為微分 d

因此，(5)式的連續化就變成

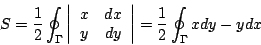$\begin{displaymath} S=\frac{1}{2}\oint_ \Gamma \left\vert\begin{array}{cc} x& dx... ...& dy \end{array}\right\vert ={\frac{1}{2}}\oint_\Gamma xdy-ydx \end{displaymath}$

(7)

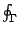此地積分記號 $\oint_\Gamma$ 意指沿 Γ 以逆時針方向作曲線積分 (line integral)。我們可以這樣來理解(6)式：想像封閉曲線 Γ 上無窮地接近的兩點 (x,y)、(x+dx,y+dy) 與原點 (0,0) 所圍成無窮小的三角形面積為

$\begin{displaymath}{1\over 2}\left\vert \begin{array}{cc} x &x+dx\\ y &y+dy \en... ...t\vert \begin{array}{cc} x &dx\\ y &dy \end{array}\right\vert \end{displaymath}$

再讓 (x,y) 沿曲線 Γ 的逆時針方向變動，連續地求和（即積分），就得到(7)式，參見圖6。

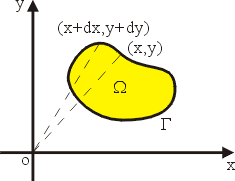
圖6

例1：

橢圓 Γ 的參數方程式為

$\begin{displaymath}\left\{ \begin{array}{lr} x=a\cos t & \\ y=b\sin t \quad & 0\le t\le 2\pi \end{array}\right. \end{displaymath}$

由(7)式算得

$\begin{eqnarray*} S&=&{1\over 2}\oint_\Gamma xdy-ydx\\ &=&{1\over 2}\int_{0}^{... ...(-a\sin t)]dt\\ &=&{1\over 2}ab\int_{0}^{2\pi}dt\\ &=&\pi ab \end{eqnarray*}$

這恰是通常熟悉的橢圓面積公式。

因此我們很有理由相信公式(7)是對的。事實上，我們可以採用一般微積分教科書上的極限論證法給予證明。不過，我們要指明：從 Leibniz 或非標準分析 (non-standard analysis) 的眼光來看，無窮小論證法是合法的（歷史上曾被宣佈為「非法的」），更漂亮而具有發現的潛力，並且足以保證(7)式是成立的。

定理2：

設 $\Gamma:t\in [a,b]\rightarrow(x(t)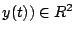$ , $y(t)) \in R^2$ 為一條單純的（即沒有打結）、封閉的可微分曲線，並且是逆時針定向，則 Γ 所圍成的領域之面積為

S	=	$\displaystyle {1\over 2}\oint_\Gamma \left\vert \begin{array}{cc} x &dx\\ y &dy \end{array}\right\vert$
	=	$\displaystyle {1\over 2}\oint_\Gamma xdy-ydx$
	=	$\displaystyle {1\over 2}\,\int_{a}^{b}[x(t)y'(t)\,-y(t)x'(t)]dt$	(8)

註：: (8)式表示，沿著曲線 Γ 繞一圈，作某種功（或度量），就知道曲線所圍的面積，這真奇妙。一位農夫沿著農地走一圈就知道面積！

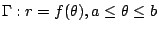對於極坐標描述的封閉曲線 $\Gamma:r=f(\theta),a\le\theta\le b$ 可改為參數方程式

$\begin{eqnarray*} \noindent\left\{ \begin{array}{l} x=f(\theta)\cos\theta\\ y=f(\theta)\sin\theta \quad\quad a\le\theta\le b \end{array}\right. \end{eqnarray*}$

計算

$\begin{displaymath}x(\theta)y'(\theta)-y(\theta)x'(\theta)=(f(\theta))^2\end{displaymath}$

於是得到：

推論：

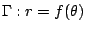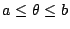設 $\Gamma :r = f(\theta)$ , $a \le \theta \le b$ , 為一條單純的、封閉的可微分極坐標曲線，則 Γ 所圍成領域之面積為

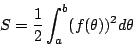$\begin{displaymath} S={1\over 2}\int_{a}^{b}(f(\theta))^2d\theta \end{displaymath}$

(9)

註：

事實上，不必限於封閉的極坐標曲線，(9)式亦成立。這是在微積分中我們熟悉的一個公式。

例2：

設 a>0，考慮半徑為 a 的圓在半徑為 3a 的圓內部沿著圓周滾動，試求滾動圓上一點 P 的軌跡所圍成領域之面積。

解：

如圖7所示，取圓心為原點，並且小圓上的 P 點起先跟 (3a,0) 點重合，然後開始滾動，再取圓心角 θ 當參數，容易算出 P 點的坐標 (x,y) 滿足

$\begin{eqnarray*} \left\{ \begin{array}{l} x = 2a\cos\theta + a\cos 2\theta\... ...ta - a\sin 2\theta,\quad 0\le\theta\le 2\pi \end{array}\right. \end{eqnarray*}$

我們稱 P 點的軌跡為圓內三尖輪迴線 (Deltoid)。由公式(8)知，它所圍成領域之面積為

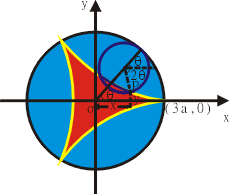
$\begin{eqnarray*} S &=& {1\over 2}\oint_\Gamma xdy-ydx\\ &=& {a^2\over 2}\int_... ...\over 2}\int_{0}^{2\pi}(2-2\cos 3\theta)d\theta\\ &=& 2\pi a^2 \end{eqnarray*}$

圖7

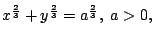習題：: 求星形線 $x^{2\over 3}+y^{2\over 3}=a^{2\over 3}, \; a>0,$ 所圍的面積。

　1│2│3│4│5│6│7　


	（若有指正、疑問……，可以在此留言或寫信給我們。）

EpisteMath (c) 2000 中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有

編輯：鄧惠文 ∕ 校對：康明軒 ∕ 繪圖：張琇惠

最後修改日期：4/26/2002