級數求和法 (第 5 頁)

　1│2│3│4│5│6　

級數求和法（第 5 頁）

余文卿

首頁 | 搜尋

．原載於數學傳播第十五卷第四期
．作者當時任職於中央研究院數學所研究員，借調至中正大學應數所
‧對外搜尋關鍵字

5. 關於 $\Gamma''(S)/\Gamma(S)$

把積分式

$\begin{displaymath}\frac{\Gamma'(1+\delta)}{\Gamma(1+\delta)}+\gamma=\int_0^\infty\frac{(1-e^\delta t)dt}{e^t-1}\end{displaymath}$

對 δ 微分，則得出

$\begin{displaymath}\frac{\Gamma''(1+\delta)}{\Gamma(1+\delta)}-\left[\frac{\Gamm... ...+\delta)}\right]^2 =\int_0^\infty\frac{te^{-\delta t}dt}{e^t-1}\end{displaymath}$

用來求出 $\Gamma'(1+\delta)/\Gamma(1+\delta)(\delta=q/p)$ 的方法已不再適用，經由 u = e^-t/p 的變數變換後，會有 $\log u$ 出現在積分裏，故除了一些特別數值外，這類數值並不易求出，為方便起見，定

$\begin{displaymath} F(\delta) = \frac{d}{d\delta} \left[\frac{\Gamma'(\delta)}{... ...lta)} - \left[\frac{\Gamma'(\delta)}{\Gamma(\delta)}\right]^2 \end{displaymath}$

由等式

$\begin{displaymath}\Gamma(s)\Gamma(1-s)=\frac{\pi}{\sin{\pi s}}\end{displaymath}$

兩邊取對數且對 s 連續微分兩次，則得

$\begin{displaymath}F(s)+F(1-s)=\pi^2\csc^2{\pi s}\end{displaymath}$

特別是

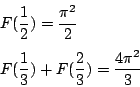
$\begin{displaymath} \begin{eqalign} & F(\frac{1}{2})=\frac{\pi^2}{2} \\ & F(\frac{1}{3})+F(\frac{2}{3})=\frac{4\pi^2}{3} \end{eqalign}\end{displaymath}$

故

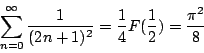
$\begin{displaymath}\sum_{n=0}^\infty\frac{1}{(2n+1)^2}=\frac{1}{4}F(\frac{1}{2})=\frac{\pi^2}{8}\end{displaymath}$

例題2:
求級數 $\sum_{n=0}^\infty\frac{1}{(3n+1)^2(3n+2)^2}$ 的和。

解答:

$\begin{eqnarray*} &&\sum_{n=0}^\infty\frac{1}{(3n+1)^2(3n+2)^2}\\ &=&\frac{1}{9... ...c{\pi}{\sqrt{3}})\\ &=&\frac{4\pi^2}{27}-\frac{2\pi}{3\sqrt{3}} \end{eqnarray*}$

　1│2│3│4│5│6　


	（若有指正、疑問……，可以在此留言或寫信給我們。）

EpisteMath (c) 2000 中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有

編輯：石莉君 ∕ 校對：康明軒

最後修改日期：4/26/2002