級數求和法 (第 4 頁)

　1│2│3│4│5│6　

級數求和法（第 4 頁）

余文卿

首頁 | 搜尋

．原載於數學傳播第十五卷第四期
．作者當時任職於中央研究院數學所研究員，借調至中正大學應數所
‧對外搜尋關鍵字

4. $\Gamma'(S)/\Gamma(S)$ 的值

在 P(x)=0 沒有重根時出現在 $\sum_{n=1}^{\infty}P(n)^{-1}$ 的和只是 $\Gamma'(1+\delta)/\Gamma(1+\delta)$ 與 $P(-\delta)^{-1}$ 的組合；在 δ 是有理數時， $\Gamma'(1+\delta)/\Gamma(1+\delta)$ 的數值可明確的表現出來，當然這數值不一定是有理數，有時會有根數或 π 跑出來。設 $\delta = q/p$ ， $p,q \in N$ ， $0<\delta<1$ ，將已知的等式

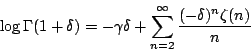
$\begin{displaymath}\log\Gamma(1+\delta) = -\gamma\delta+\sum_{n=2}^{\infty}\frac{(-\delta)^n\zeta(n)}{n}\end{displaymath}$

對 δ 微分，即得出

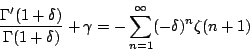
$\begin{displaymath}\frac{\Gamma'(1+\delta)}{\Gamma(1+\delta)}+\gamma=-\sum_{n=1}^{\infty}(-\delta)^n\zeta(n+1)\end{displaymath}$

另一方面，由

$\begin{displaymath}\zeta(n+1)\Gamma(n+1)=\int_{0}^{\infty}\frac{t^n}{e^t-1}dt\end{displaymath}$

也得出

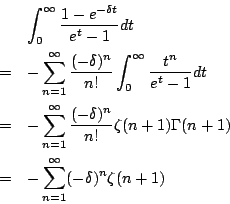
$\begin{eqnarray*} &&\int_{0}^{\infty}\frac{1-e^{-\delta t}}{e^t-1}dt\\ &=&-\sum... ...(n+1)\Gamma(n+1)\\ &=&-\sum_{n=1}^{\infty}(-\delta)^n\zeta(n+1) \end{eqnarray*}$

故

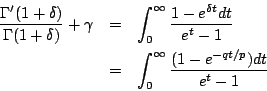
$\begin{eqnarray*} \frac{\Gamma'(1+\delta)}{\Gamma(1+\delta)}+\gamma &=&\int_{0}^... ...}dt}{e^t-1}\\ &=&\int_{0}^{\infty}\frac{(1-e^{-qt/p})dt}{e^t-1} \end{eqnarray*}$

經由 u=e^-t/p 的變數變換，得出

$\begin{eqnarray*} \frac{\Gamma'(1+q/p)}{\Gamma(1+q/p)}+\gamma &=& p\int_0^1\fra... ...]du\\ &=&\frac{p}{q}+p\int_0^1\frac{(u^{p-1}-u^{q-1})du}{1-u^p} \end{eqnarray*}$

移項得出

$\begin{displaymath}\frac{\Gamma'(q/p)}{\Gamma(q/p)}+\gamma=p\int_0^1\frac{(u^{p-1}-u^{q-1})du}{1-u^p}\end{displaymath}$

注意到

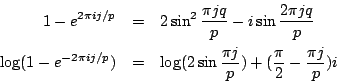
$\begin{eqnarray*} 1-e^{2\pi ij/p} &=& 2\sin^2{\frac{\pi jq}{p}}-i\sin{\frac{2\pi... ...\log(2\sin{\frac{\pi j}{p}}) + (\frac{\pi}{2}-\frac{\pi j}{p})i \end{eqnarray*}$

取實部即得出

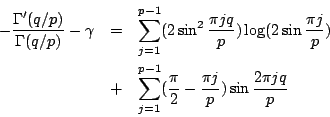
$\begin{eqnarray*} -\frac{\Gamma'(q/p)}{\Gamma(q/p)}-\gamma &=&\sum_{j=1}^{p-1}(2... ...j=1}^{p-1}(\frac{\pi}{2}-\frac{\pi j}{p})\sin{\frac{2\pi jq}{p}} \end{eqnarray*}$

特別在 p=2, 3 時，由上式得出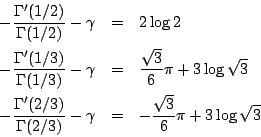

$\begin{eqnarray*} -\frac{\Gamma'(1/2)}{\Gamma(1/2)}-\gamma &=&2\log2\\ -\frac{\... .../3)}{\Gamma(2/3)}-\gamma &=&-\frac{\sqrt{3}}{6}\pi+3\log\sqrt{3} \end{eqnarray*}$

運用到級數 $\sum_{n=0}^{\infty}\frac{1}{(3n+1)(3n+2)}$ 上面，則得出

$\begin{eqnarray*} &&\sum_{n=0}^{\infty}\frac{1}{(3n+1)(3n+2)}\\ &=&\frac{1}{9}\... ...ac{\Gamma'(2/3)}{\Gamma(2/3)}\right]\\ &=&\frac{\pi}{3\sqrt{3}} \end{eqnarray*}$

又

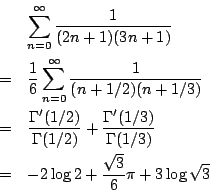
$\begin{eqnarray*} &&\sum_{n=0}^{\infty}\frac{1}{(2n+1)(3n+1)}\\ &=&\frac{1}{6}\... ...}{\Gamma(1/3)}\\ &=&-2\log2+\frac{\sqrt{3}}{6}\pi+3\log\sqrt{3} \end{eqnarray*}$

　1│2│3│4│5│6　


	（若有指正、疑問……，可以在此留言或寫信給我們。）

EpisteMath (c) 2000 中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有

編輯：石莉君 ∕ 校對：康明軒

最後修改日期：4/26/2002