�D�����ƾǶǼ��ĤT���ĤG��
�D�@�̷��ɴNŪ�����d�D���j��
�E����
�i����
|
|
�D�����ƾǶǼ��ĤT���ĤG�� �D�@�̷��ɴNŪ�����d�D���j�� �E���� | ||
|
��Ψ�U���ܧιC��
�i���� |
|
�N�����z�����@�e��z�@�ˡA�ƾǹC��������ʩM��ƾDzz�ת�����ʡA�������۱ƥ����ⳡ���C�@�عC�������Q�ƾǨM�w�H��A�����H�u�n��o�䤤���z�סA�L���B���u�աC�C�������h�����ƾǪ��p��A���_�ӥ����M�L���F���p�G�N�������ƾǰ��D�B�z�A�hĭ�æ��Ʀh�������z�צb�䤤�C�I���D�ԩʪ��C���A�h�S���T�w���W�ߥi�M�A�����H�����ܡA�a�{���������M�H�����g����ӡA���̦����F���b�ƾDzz�פW�h�S������i���C
��Ψ�U���ܫ��C���j���ݩ�e�̡C�����@�ؾǰݡA�ڭ̥u���ߨ�I��������ƾDzz�סC
�b�Ҧ����H�什�C�����A��O����j�ѥB�ǴI���쪺�@�ӽ��D�C�ڻ��A��ۤ���A�g�ѳQ�c�����w�����u�̥~�ǡC���W���u�H�̡A�b�u�@���v���l�A�Υ��Y���C���H�ƻ��I��C�y�Ǩ찪�ŤH�h�A�h�ο�h (Pennils)�A�b�s�a�d�i�W���C
�̦��W���O�N�Q�G�T��h���T�C�Ʀ��u�T�B�|�B���v���C���A�p�U�ϡG
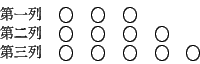
�C�����W�h��²��C��H���y���ɪO�A�C�H�C���ݦb�Y�@�C���@�T�Τ@�T�H�W���ɪO�A������P�ɦb��C���ɪO�A����̫�A�N�ɪO�������HĹ�o���C���C �]�i�H���ۤϪ��W�w�G�̫�N�ɪO�������H��C
�@���Y���F������Ҥ��[�N�|�o�{�A�������H�A�b�Ĥ@�C���T�T�ɪO�������G�T�A�N��í�Ӻ�C�@����ө������W�߬O�A�u�n�A�d�U��C�T�ƬۦP���ɪO�A���i��ӡC�b�o�ع�٧�t�����n������C �p�G�o�ӹC���u�O�u�T�B�|�B���v���A�A���[��A�j�����H�N����x�䤤�W�ߡA�åB�ܱo�S������C���@�ӧ��ܪ���k�O�A�N�ɪO���C�ƼW�[�A�C�@�C���T�Ƨ��ܡC�o�˪����k�A���T�ϤH���@�L�W�ߪ��Pı�A�ܤ֤��ܩu�T�B�|�B���v���A����@�˩���ⴤ�C
���쥻�@����A����j�ǼƾǨt�Ʊб¬d�z�h�D�z���Ǽw�D�]�y (Chales Leonard Bouton) ���X�@�g���Ժɪ����R�M�ҩ��A�Q�μƪ��G�i����ܪk�A�ѵ��F�o�ӹC�����@��k�h�G����N�C�ƪ��ɪO�A�C�C�����N�T�ơA�p����o�P�Ӥ��D�H
�b�]�y���N�y���A���L��ѤU���ݧ����O�w�� (safe) �N�O���w�� (unsafe) �������C�b�Ҧ��w�������p�U�A�����p���`�O��@���w�������p�A�A�i�H�A���A���T�ƪ��ɪO�]�b�A�����Y�@�C�^�A�F��t�@�w�������p�A�o�ˤ@���쮳���ɪO����A���M�̫�@�������ɪO���@�w�O�A�C�Ϥ��A�A�p�G�d�U���w�������p�A��襲����k�b�A�����Y�@�C�A�����A���T�ƪ��ɪO�A�F��L���w�����p�A�]�N�O���A��w�F�C
�]�y����k��²��C�����A�N�U�C�ɪO���T�ƤƦ��G�i��ơA�ۥ[�A�����i��A�M��A�ݩM���U�Ӧ�ơC�p�G�M���U�Ӧ�Ƴ��O���ơA�h���ܤ@�w���ݧ�;�_�h�A�p�G���@��O�_�ơA�h�����w���ݧ��C�Ҧp�u�T�B�|�B���v�C���A�@�}�l�N�O���w���ݧ��A�������H�i�H�A�����G�T�ӳy���L���w���ݧ��C
�t�@�Ӥ��w���ݧ����Ҥl�p�U�G
������w���ݧ��M���w���ݧ��i�H�Q�ΤW�z����k�P�w�O�H�o�ӹD�z����²��C�����A�p�G�N�U�C�ɪO�ƤƬ��G�i����ܪk�A�ۥ[�A�����i��A�o�쪺�U�Ӧ�Ƴ��O���ƪ��ܡA���������@�C�A�h�֪T�ɪO�A�h���@�C�ɪO�Ʃҹ������G�i����ܪk���A�����Y�@��μƦ�� 0 �ܦ� 1 �Ϊ̥� 1 �ܦ� 0�A
��ۥ[���M�]�۹諸���Y�@��μƦ�Ѱ����ܦ��_�ơC�Ҧp�A{1,4,5}�o�Ӧw���ݧ��A�q�ĤG�C�� 4 �T�ɪO���� 2 �T�A�h
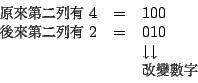

�ۤϪ��A�p�G�M���Y�@��μƦ�O�_�ơA�h�ڭ̦���k�b�Y�@�C�����A���T�ƪ��ɪO�A�ϱo�s���M���U�Ӧ�Ƴ��O���ơC �����A����M���Ҧ����_�ƪ��U�Ӧ��
�ۤϳW�w�A�����ɪO���H���ϡA�u�A�N�W�����W�߲��[���A�]�i�H������C�p�G�A�@���֦��w���ݧ��A���@���B�w�������p�A��Y�@�ɭԡA���d�U�Ӫ����w���ݧ��@�w�|�X�{�@�دS�����A�A�Y�O�A���Y�@�C�ɪO���T�Ƥj�� 1�A��L�U�C���u���@�T�ɪO�]�������U�C���ޥ��^�A�o�ɭԧA�����k�n�}�l�`�N�A �A�ݱN���h�T�ɪO�o�@�C���������A�Ϊ̮���u�ѤU�@�T�A�M�w�Ĩ���̡A�����ݧA���F����A�n��ϳѤU���C�Ƭ��_�ơA���M�C�@�C���u���@�T�ɪO�C��ө������O�A�H��@�H�����@�C�A�]�O�@�T�A��̫᮳���@�w�O���A��O�A�NĹ�F�C
���ܦh�H��o�Ӥ�k�g���q���{���A�өM�H��ܡA�����N�z���H�Q�F�o�ι���A�L����Ĺq�������_���j�C��껡��F�A�u�]�����p���H�֡A�ƪ���Ƭ��G�i���t�קֱo�D�H���A�p���}�F�C
|
��~�j�M����r�G �D�O��ƦC �D�i��k |
|
|
|
|
�]�Y�������B�ðݡK�K�A�i�H�b�� �d�� �� �g�H ���ڭ̡C�^ |
|
|
|
EpisteMath (c) 2000 ������s�|�ƾǩҡB�x�j�ƾǨt �U�����峹���e���ۧ@�v����ۧ@�H�Ҧ� |
| �s��G������ | �̫�ק����G4/26/2002 |