拈及其各種變形遊戲 (第 3 頁)

　1│2│3│4│5│6　

拈及其各種變形遊戲（第 3 頁）

張鎮華

首頁 | 搜尋

．原載於數學傳播第三卷第二期
．作者當時就讀於美國康乃爾大學

‧註釋
‧對外搜尋關鍵字

(三)費氏數列及進位法

費氏數列是指無窮數列 1,2,3,5,8,13,21,… 而言，它的一般表示式是 f₀=1，f₁=2， f_n+2=f_n+1+f_n 真正把它計算出來是

$\begin{displaymath} f_n=\frac{1}{\sqrt{5}} \Big\{ (\frac{1+\sqrt{5}}{2})^{n+2}-(\frac{1-\sqrt{5}}{2})^{n+2} \Big\} \end{displaymath}$

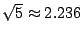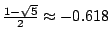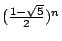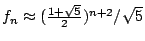計算的過程和我們要討論的沒有太大關係，茲從略。有一點可以注意的是，{f_n} 幾乎成一等比級數。因為 $\sqrt{5} \approx 2.236$ , $\frac{1-\sqrt{5}}{2} \approx -0.618$ ，其絕對值小於 1，當 n 很大時， $(\frac{1-\sqrt{5}}{2})^n$ 變得很小，幾乎可以省略不計。也就是說 $f_n \approx (\frac{1+\sqrt{5}}{2})^{n+2}/\sqrt{5}$ ，幾乎是等比級數型式增加。

費氏級數最有趣的特性是，自然界許多生長的過程或多或少和它有點關聯。可參考《數學漫談》第四章（下）。

通常我們所熟悉的阿拉伯數字表示自然數的方法是利用 0,1,2,3,4,5,6,7,8,9 十個數字為基礎，借「位」的觀念，和「逢十進一」的方法組織而成。這就是十進位法。舉例來說， 345=3 x 10²+4 x 10¹+5。仿照這個道理，有各種進位法，例如電腦所熟悉的二進位法，僅有 0 和 1 兩種基本數字，10110表示 1 x 2⁴ + 0 x 2³ + 1 x 2² + 1 x 2¹ + 0 = 16+4+2 = 22。八進位法，則僅有 0,1,2,3,4,5,6,7 八個數字。

標準的進位法中，各位都是滿一個固定數就進位。例如：十進位法是滿十進一，即個位數滿十進一到十位數，十位數滿十進一到百位數，百位數滿十進一到千位數，……等。

考慮一個自然數的無窮數列 B₀,B₁,B₂,… 其中 B₀=1，其餘各 B_n 均大於 1。我們可以採取一種名為 B 進位法的記數法則：由右邊算起，第一位滿 B₁ 進一到第二位，第二位滿 B₂，進一到第三位，……，第 n 位滿 B_n，進一到第 n+1位。

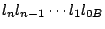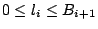任何一個自然數 x 可以有唯一的 B 進位表示法 $l_nl_{n-1}\cdots l_1l_{0B}$ ，其中 $0\leq l_i\leq B_{i+1}$ 。則

$\begin{displaymath} x=l_nl_{n-1}\cdots l_1l_{0B}=\sum_{m=0}^nl_m(B_0B_1\cdots B_m) \end{displaymath}$

標準十進位法是取 B_i=10, i=1,2,…。各種 k 進位法是指 B_i=k, i=1,2,…而言。

[例6] B_n=n+1，求347的 B 進位表示法。

$\begin{displaymath} \begin{array}{rccrcl} 2\vert\underline{347}&&\mbox{\hskip 1... ...{14}&\cdots 1 & & 14 &=& 2\times5+4\\ 2&\cdots4&& \end{array}\end{displaymath}$

所以 347 = 2 x (2 x 3 x 4 x 5) + 4 x (2 x 3 x 4) + 1 x (2 x 3) + 2 x 2+1=24121_B

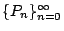假設 P_n=B₀ B₁ … B_n 則 $\{P_n\}_{n=0}^{\infty}$ 成為一個以 1 為起點的嚴格遞增無窮自然數列。自然數 N 的 B 進位表示法

$\begin{displaymath} l_nl_{n-1}\cdots l_1l_{0B}=\sum_{m=0}^{n}l_mP_m,\quad \mbox... ...{m}\selectfont \char 50}}0\leq l_i<\frac{P_{i+1}}{P_i}=B_{i+1} \end{displaymath}$

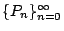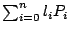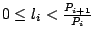如果我們一開始就取一個以 1 為起點的嚴格遞增無窮自然數列 $\{P_n\}_{n=0}^{\infty}$ ，對於任何自然數 N 表示成 $\sum_{i=0}^{n}l_iP_i$ , $0\leq l_i<\frac{P_{i+1}}{P_i}$ 有無困難？答案是有的。在 B 進位表示法中，每一個自然數恰有唯一的一種表示法；但是在這種新的表示法中，不一定每個自然數均只有一種表示法。

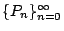[例6.1] 數列 $\{P_n\}_{n=0}^{\infty}$ 定義為 P_n=2n+1, 則

$\begin{displaymath} 8=7+1=P_3+P_0=1001(P),\quad 8=5+3=P_2+P_1=110(P) \end{displaymath}$

有趣的是，自然數的 P 數列表示法一定有解。

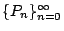[定理2] $\{P_n\}_{n=0}^{\infty}$ 是一個以 1 為起點的嚴格遞增無窮自然數列，則每一自然數 N 至少可以表示成一種 P 數列表示法

$\begin{displaymath} l_nl_{n-1}\cdots l_1l_0(P)=\sum_{i=0}^nl_iP_i, \quad \mbox{... ...tseries{m}\selectfont \char 50}} 0\leq l_i<\frac{P_{i+1}}{P_i} \end{displaymath}$

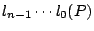[證] 利用數學歸納法證明：N<P_n 時 N 有 P 數列表示法 $l_{n-1}\cdots l_0(P)$ 。

n=1 時，N=l₀，其中 l₀(P)=N。若 n=k 時本定理成立，則 n=k+1 時，利用除法公式，可以找到 l_k 及 r 使得

$\begin{displaymath} N=l_kP_k+r, \quad 0\leq r<P_k, \quad \mbox{{\fontfamily{cwM... ...ont \char 248}}0\leq l_k\leq \frac{N}{P_k}<\frac{P_{k+1}}{P_k} \end{displaymath}$

由歸納法假設

$\begin{displaymath} r=l_{k-1}\cdots l_1l_0(P)=\sum_{i=0}^{k-1}l_iP_i, \end{displaymath}$

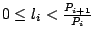而且 $0\leq l_i<\frac{P_{i+1}}{P_i}$ 。故

$\begin{displaymath} N=\sum_{i=0}^kl_iP_i=l_kl_{k-1}\cdots l_1l_0(P), \quad \mbo... ...ntseries{m}\selectfont \char 47}}0\leq l_i<\frac{P_{i+1}}{P_i} \end{displaymath}$

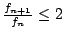將上面這種理論用到費氏數列 {f_n} 因為 $\frac{f_{n+1}}{f_n}\leq2$ ，所以費氏表示法中的各個「位數」只能是 0 或 1。費氏數列表示法不具有唯一性。

[例7] 化60為費氏數列表示法。

n	0	1	2	3	4	5	6	7	8
f_n	1	2	3	5	8	13	21	34	55

$\begin{eqnarray*} 60&=&f_8+f_3=1000010000(f)\\ &=&f_7+f_6+f_2+f_1=11000110(f)\\ &=&f_7+f_5+f_4+f_2+f_1=10110110(f) \end{eqnarray*}$

因為 f_n+2=f_n+1+f_n，費氏數列表示法中有一種有趣的「進位法」：第 n 位和第 n+1 位都是 1 時，可以進位到第 n+2 位。如上例 10110110(f) 的第 5 和第 6 位都是 1，故可以進位到第 7 位，將原數化成 11000110(f)；同理，可將 11000110(f) 的第 2 和第 3 位進位到第 4 位，成為 11001000(f)。利用這個性質，在一數的某一費氏數列表示法中，如果有相鄰的兩位均是 1，則可以進位到左邊一位，化成另一個不同的表示法，繼續化簡，到最後，可以得到一種表示法，其中 l_i 各數目，相鄰兩個不同時為 1（否則，再進位即可），每一個數都有一種唯一的如此表示法，稱之為標準表示法。

另一有趣的性質是：如果 l_nl_n-1 … l₁l₀(f) 中各位數字 0 和 1 相間出現，例如 101010(f) 或 10101(f) 則

$\begin{displaymath} l_nl_{n-1}\cdots l_1l_0(f)+1(f) = 1\underbrace{00 \cdots 00... ...ily{cwM0}\fontseries{m}\selectfont \char 95}} 0} (f) = f_{n+1} \end{displaymath}$

　1│2│3│4│5│6　


	（若有指正、疑問……，可以在此留言或寫信給我們。）

EpisteMath (c) 2000 中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有

編輯：李渭天

最後修改日期：4/26/2002