認識連分數 (第 5 頁)

　1│2│3│4│5│6│7　

認識連分數（第 5 頁）

林聰源

首頁 | 搜尋

．原載於數學傳播第二卷第三期
．作者當時任教於清大數學系
‧對外搜尋關鍵字

§4. 無窮連分數

古希臘之神殿 Parthenon 結構之美，嘆為觀止，常謂之「黃金比」或「黃金分割」，其確實意義如下：

假定有一個長方形，截掉一正方形後，所剩之小長方形與原長方形相似（見圖一），則從此小長方形依樣再截掉一小正方形，所剩之圖形仍與原長方形相似，這種程序可無窮盡地做下去，這就叫做「黃金分割」，而具備此種特性之長方形之長寬比稱為「黃金比」。

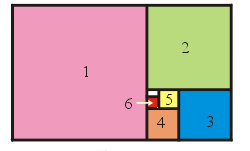
圖一

那黃金分割又怎麼和連分數扯上關係呢？

讓我們先看一下黃金比的計算：

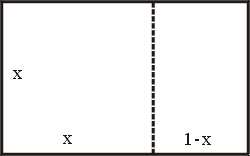
圖二

設圖二長方形之長邊為單位長 1，而短邊長為 x，則根據假設

1:x=x:(1-x),

即

x²+x-1=0

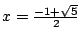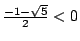解出 $x=\frac{-1+\sqrt{5}}{2}$ （另一根 $\frac{-1-\sqrt{5}}{2}<0$ 不合），此數即為黃金比，為一無理數，其近似值為 0.618。所以平常也有人說黃金比是 3:5=0.6 的。現在換一個角度來看 x 的求法：方程式 x²+x-1=0 可化為

$\begin{displaymath} x=\frac{1}{1+x} \end{displaymath}$

將此式帶入其本身右邊的 x 中，便得

$\begin{displaymath} x=\frac{1}{1+(\frac{1}{1+x})} \end{displaymath}$

繼續不斷此步驟，則得

$\begin{displaymath} x=\frac{1}{\displaystyle 1 + \frac{1}{\displaystyle 1 + \frac{1}{\displaystyle 1 + \ddots }}} \end{displaymath}$

這就是無窮連分數的一個例子。我們看一下它的頭幾個漸近分數：

$\begin{displaymath} \begin{eqalign} & \frac{1}{1}=1, \quad \frac{1}{1} \; \lower... ...rac{1}{1} = \frac{8}{13}=0.615\cdots, \;\; \cdots \end{eqalign}\end{displaymath}$

由此可知利用連分數來求此種二次方程式的無理數是一個非常有價值的辦法。一般而言，一個型如

$\begin{displaymath} a_0 + \frac{1}{\displaystyle a_1 + \frac{1}{\displaystyle a_2 + \ddots}} \end{displaymath}$

的式子稱為無窮連分數，簡寫成

$\begin{displaymath} a_0 + \frac{1}{a_1} \; \lower1.5ex\hbox{$+$}\; \frac{1}{a_2}... ...fontseries{m}\selectfont \char 67}} \quad [a_0,a_1,a_2,\cdots] \end{displaymath}$

通常我們只考慮 a₀ 為整數而 a₁,a₂,… 為正整數的情形，這又特別叫做簡單無窮連分數。就像每一個有理數都可以用簡單有窮連分數表示（如 §1. 所示）一樣，每一個實數也都可以用簡單無窮連分數表示，其法如下：

設 ξ 為任意一實數，則

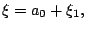$\xi=a_0+\xi_1,$ 其中 a₀ 為整數而 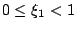$0\leq\xi_1<1$ （此種表法為唯一）。

若 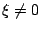$\xi\neq0$ ，則

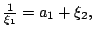$\frac{1}{\xi_1}=a_1+\xi_2,$ 其中 a₁ 為整數而 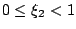$0\leq\xi_2<1$ （此種表法為唯一）。

這種步驟反覆進行，若 ξ 非有理數，則程序不終止，而得一簡單無窮連分數。無窮連分數之漸近分數滿足 §2. 推論中所有的性質，我們有：

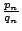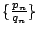命題：設 $\frac{p_n}{q_n}$ 表無窮連分數 $[a_0,a_1,a_2\cdots]$ 之第 n 個漸近分數，則數列 $\{\frac{p_n}{q_n}\}$ 收斂。若其收斂值為 ξ，則 $[a_0,a_1,a_2\cdots]$ 即為 ξ 之無窮連分數表示。

證明：由 §2. 之推論，已知

$\begin{displaymath} \frac{p_0}{q_0}<\frac{p_2}{q_2}<\frac{p_4}{q_4}<\cdots \eqno{(\mbox{I})} \end{displaymath}$

$\begin{displaymath} \frac{p_1}{q_1}>\frac{p_3}{q_3}>\frac{p_5}{q_5}>\cdots \eqno{(\mbox{II})} \end{displaymath}$

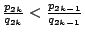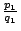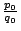而且由推論 2， $\frac{p_{2k}}{q_{2k}}<\frac{p_{2k-1}}{q_{2k-1}}$ 所以數列(I)有一上界 $\frac{p_1}{q_1}$ ，而數列(II)有一下界 $\frac{p_0}{q_0}$ ，由單調數列之收斂性，(I)與(II)皆收斂。再由推論 2，(I)與(II)之收斂值是相同的，這就證明了漸近分數數列 {p_n/q_n} 之收斂性。

命題後半之證明從略。事實上，漸近分數是所有分母不超過 q_n 的分數中最接近者，也就是說它們是 ξ 的最佳漸近分數。（參考《數論導引》pp. 270-272）。我們也明白地看出所有偶數次項皆比收斂值小，而奇數次項皆比收斂值大。

　1│2│3│4│5│6│7　


	（若有指正、疑問……，可以在此留言或寫信給我們。）

EpisteMath (c) 2000 中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有

編輯：李渭天 ∕ 繪圖：簡立欣

最後修改日期：4/26/2002