| |
現在考慮一般有窮連分數的幾個基本關係式。設
為任意一個一般的有窮連分數(也就是說
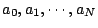 為任意非零之實數),由計算易得 為任意非零之實數),由計算易得
一般地
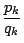 稱為此連分數之第 k 個漸近分數,我們有 稱為此連分數之第 k 個漸近分數,我們有
- 公式 1:
- 證明:
利用歸納法
- 公式 2:
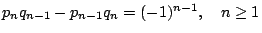 。 。
- 證明:
利用歸納法,n=1 時,
p1q0-p0q1 = (a0a1+1) x 1-a0 x a0=1
又
- 公式 3:
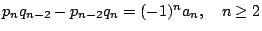 。 。
- 證明:
利用歸納法,n=2 時,
p2q0-p0q2=(a2a1a0+a2+a0 x 1-a0 x (a2a1+1)=a2
又
在實際應用中,我們所遭遇的有窮連分數,就像(丙)式一樣,其中的 a0 為整數,a1,a2,…,aN 皆為正整數,此種連分數特稱為簡單有窮連分數。由以上公式,我們可推論出有關此等簡單有窮連分數的幾個基本性質。
- 推論 1:
當 k>1 時,
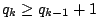 ,故 ,故 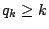 。 。
- 證明:
由公式 1,
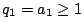 ,又 ,又
由歸納法得 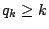 。 。
- 推論 2:
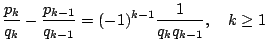
- 證明:
由公式 2,兩邊除以 qkqk-1 即得。
- 推論 3:
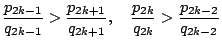
- 證明
由公式 3,兩邊除以 qkqk-1,即得
當 n=2k 為偶數時,右式為正,故得
當 n=2k+1 為奇數時,右式為負,故得
- 推論 4:對所有
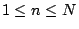 ,pn 與 qn 互質。 ,pn 與 qn 互質。
- 證明:
由公式 1 立可得知。
從以上幾個推論,我們知道漸近分數的分母一直增大,而兩相鄰漸近分數之差則愈來愈小。另外,偶數項部分形成單調嚴格上昇數列而奇數項部分形成單調嚴格下降數列,在第4節討論無窮連分數時,這些性質對收斂性非常重要。
|
|
|