Green 定理與應用 (第 6 頁)

　1│2│3│4│5│6│7　

Green 定理與應用（第 6 頁）

林琦焜

首頁 | 搜尋

．原載於數學傳播第二十一卷第四期
．作者當時任教於成功大學數學研究所
‧對外搜尋關鍵字

六、線積分的微積分基本定理

在第五節我們引進了位能函數 (potential function) $F=\nabla \phi$ 之概念，實際上可經由全微分 (total differential) 來理解

$\begin{displaymath} \left\{ \begin{array}{l} F\cdot d \overrightarrow{r} = P d... ...r} = \nabla \phi \cdot \overrightarrow{r} = d \phi \eqno{(30)} \end{displaymath}$

因此

$\begin{displaymath} P= \phi_x, \; Q=\phi_y, \quad \Rightarrow{} \quad P_y = Q_x \end{displaymath}$

換為微分方程的語言則是「正合」(exact)。

線積分的微積分基本定理：假設 $\phi$ 為一可微分函數，且其梯度 $\nabla \phi$ 為連續， $\overrightarrow{r}$ 為連接 $\overrightarrow{a},\overrightarrow{b}$ 兩點之任意曲線，則

$\begin{displaymath} \int_{\overrightarrow{a}}^{\overrightarrow{b}} \nabla \phi \... ...\phi(\overrightarrow{b})-\phi(\overrightarrow{a}) \eqno{(31)} \end{displaymath}$

這定理的物理意義（電學的角度）：沿著電場上兩點間任一曲線電場所作的功為兩點的電位差，由 Green 定理可知若 $F=\nabla \phi$ ，C₁,C₂ 為連接 $\overrightarrow{a},\overrightarrow{b}$ 之任意兩條曲線則

$\begin{eqnarray*} \oint_C F\cdot d\overrightarrow{r} &=& \int_{C_1} F \cdot d \... ...l{R}} \nabla \times (\nabla \phi) \cdot \overrightarrow{k}dxdy=0 \end{eqnarray*}$

因此

$\begin{displaymath} \int_{C_1} F \cdot d \overrightarrow{r} = \int_{C_2} F \cdot d\overrightarrow{r} \end{displaymath}$

即線積分與路徑無關 (path-independent)，換句話說，將一物體（或質點）由位置 $\overrightarrow{a}$ 移至位置 $\overrightarrow{b}$ ，力對物體（質點）所作的功，僅和物體（質點）起點位置及終點位置有關，而與其運動所遵循的運動路徑無關，此時我們稱向量場 F 為保守的 (conservative)，而 $\phi$ 則稱為 F 之位能函數，這定理也告訴我們

$\begin{displaymath} \phi(\overrightarrow{x})-\phi(\overrightarrow{a})= \int_{\ov... ...}^{\overrightarrow{x}} F \cdot d\overrightarrow{r} \eqno{(32)} \end{displaymath}$

即位能函數可藉由保守力的線積分而得。

動能定理：

$\overrightarrow{r}(t)=(x(t),y(t))$ 可視為位置向量函數，則速度與加速度分別是：

$\begin{displaymath} \begin{array}[b]{lll} \overrightarrow{v}(t) = & \frac{d\over... ...2x}{dt^2} , \frac{d^2y}{dt^2} \right ) \end{array} \eqno{(33)} \end{displaymath}$

設物體的質量為 m，其所受外力的合力為 F，則由牛頓定律知

$\begin{displaymath} F=m \overrightarrow{a}= m \frac{d^2 \overrightarrow{r}}{dt^2} \eqno{(34)} \end{displaymath}$

則對 F 而言從 $\overrightarrow{r}(t_1)$ 至 $\overrightarrow{r}(t_2)$ 所作的功為

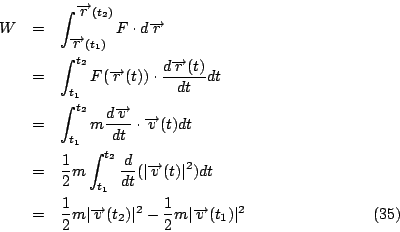
$\begin{eqnarray*} W&=&\int_{\overrightarrow{r}(t_1)}^{\overrightarrow{r}(t_2)} F... ...rrightarrow{v}(t_1)\vert^2 \qquad\qquad\qquad\qquad \eqno{(35)} \end{eqnarray*}$

其中 $\frac{1}{2}m \vert\overrightarrow{v}(t)\vert^2$ 為動能 (kinetic energy)，因此(35)式就是「動能定理」，其物理意義：

合力對物體所作的功等於動能的改變量。

如果 F 為一保守力場， $F=-\nabla \phi$ 則由線積分的微積分基本定理知：

$\begin{displaymath} W= -\phi(t_2)+\phi(t_1) \eqno{(36)} \end{displaymath}$

則(32)式改寫為

$\begin{displaymath} \phi(t_1)+\frac{1}{2}m \vert\overrightarrow{v}(t_1)\vert^2 ... ...)+\frac{1}{2}m \vert\overrightarrow{v}(t_2)\vert^2 \eqno{(37)} \end{displaymath}$

其中 $\phi$ 為位能 (potential energy)，因此(37)式就是能量守恆定律 (conservation of energy)。

散度之物理意義：

有了速度的概念之後，我們覺得這是很好的時機來闡釋散度 (divergence) 的物理意義。我們可以這麼想像：假設正在喝咖啡，將奶精倒入杯內，最初形成的圖形為 $\Omega_0$ ，而後經由攪拌或其他因素使得 $\Omega_0$ 變化，其位置向量為 $(x(t),y(t))=(\xi,\eta)$ ，速度則為 $\overrightarrow{v}(t) = (\frac{dx}{dt}, \frac{dy}{dt})=(u,v)$ ，經過 t 時間之後 $\Omega_0$ 轉換為 $\Omega_t$ ，我們有興趣的問題是 $\Omega_0$ 與 $\Omega_t$ 兩者之面積變化為何？（實際上牛頓力學本身就是一種座標變換）我們看其中一小塊 $(dV_0 \rightarrow{} d V_t)$ 兩者關係為

$\begin{displaymath} dV_0=dxdy=\frac{\partial(x,y)}{\partial(\xi,\eta)}d\xi d\eta \\ =J(t)d\xi d\eta = J(t)dV_t \eqno{(38)} \end{displaymath}$

其中 J(t) 就是 Jacobian

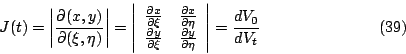
$\begin{displaymath} J(t)= \left \vert\frac{\partial(x,y)}{\partial(\xi,\eta)} \r... ... \\ \end{array} \right \vert = \frac{dV_0}{dV_t} \eqno{(39)} \end{displaymath}$

因此 $\Omega_0 \rightarrow \Omega_t$ 之變化情形，等於是探討 J(t) 的變化，我們假設 $J,J^{-1} \neq 0$ ，即沒有退化的情形（可設 $0<J<\infty$ ）：由全微分 (total differential) 知

$\begin{displaymath} \frac{d}{dt}(\frac{\partial x}{d \xi})= \frac{\partial}{\par... ... \frac{\partial u}{\partial y} \frac{\partial y}{\partial \xi} \end{displaymath}$

同理可得

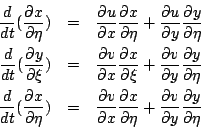
$\begin{eqnarray*} \frac{d}{dt} ( \frac{\partial x}{\partial \eta}) &=& \frac{\pa... ...+ \frac{\partial v}{\partial y} \frac{\partial y}{\partial \eta} \end{eqnarray*}$

J(t) 對 t 微分並利用行列式之性質可得

$\begin{eqnarray*} \frac{d J}{dt}&=& \left \vert \begin{array}{cc} \frac{d}{dt}\f... ...al y} \right ) J(t) \\ &=& \nabla \cdot \overrightarrow{v} J(t) \end{eqnarray*}$

所以 J(t) 滿足一階微分方程；

Euler 展開公式：

$\begin{displaymath} \frac{d J}{dt}= (\nabla \cdot \overrightarrow{v})J \quad \Lo... ...rac{d \ln J}{dt} = \nabla \cdot \overrightarrow{v} \eqno{(40)} \end{displaymath}$

這公式稱為 Euler 展開公式 (Euler expansion formula)，由微分方程知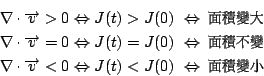

$\begin{displaymath} J(t)=e^{t(\nabla\cdot\overrightarrow{v})} J(0) \eqno{(41)} \end{displaymath}$

由此式顯然可得

$\begin{eqnarray*} \nabla \cdot \overrightarrow{v} > 0 \Leftrightarrow J(t) > J(... ...inus0.1pt{\fontfamily{cwM0}\fontseries{m}\selectfont \char 252}} \end{eqnarray*}$

因此我們稱一流體為不可壓縮 (incompressible) 其真實意義：

流體經過任何的變換其形狀雖然改變了，但其面積（或體積）卻始終保持不變。

旋度之物理意義：

由例題3 的經驗知線積分

$\begin{displaymath} \oint_C F \cdot d \overrightarrow{r} = \oint_c udx +vdy = \int \!\! \int_{\mathcal{R}} (v_x-u_y)dA \end{displaymath}$

為向量場 F=(u,v) 環繞封閉曲線 C 之環流，利用等式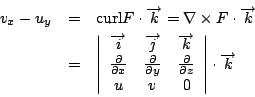

$\begin{eqnarray*} v_x - u_y &=& \mbox{curl} F \cdot \overrightarrow{k}= \nabla \... ...\ u & v &0 \\ \end{array}\right \vert \cdot \overrightarrow{k} \end{eqnarray*}$

我們可將前一式表為

$\begin{displaymath} \oint_C F \cdot d \overrightarrow{r} = \int \!\! \int_{\mathcal{R}} (v_x-u_y)dA \end{displaymath}$

假設 $\mathcal{R}$ 為包含 P₀(x₀,y₀) 之區域，則

$\begin{displaymath} \frac{1}{\vert\mathcal{R}\vert} \oint_C F \cdot d \overrightarrow{r} \end{displaymath}$

表示單位面積之環流，因此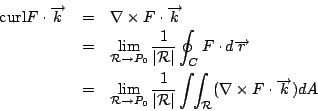

$\begin{eqnarray*} \mbox{curl} F \cdot \overrightarrow{k} &=& \nabla \times F \cd... ... \int_{\mathcal{R}} (\nabla \times F \cdot \overrightarrow{k})dA \end{eqnarray*}$

所以向量場 F 之旋度 $\nabla \times F$ （在 (x₀, y₀) 之旋度）就是單位面積產生最大環流的量且其方向垂直於 $\mathcal{R}_0$ 。

　1│2│3│4│5│6│7　


	（若有指正、疑問……，可以在此留言或寫信給我們。）

EpisteMath (c) 2000 中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有

編輯：朱安強 ∕ 繪圖：簡立欣

最後修改日期：4/26/2002