Green 定理與應用 (第 4 頁)

　1│2│3│4│5│6│7　

Green 定理與應用（第 4 頁）

林琦焜

首頁 | 搜尋

．原載於數學傳播第二十一卷第四期
．作者當時任教於成功大學數學研究所
‧對外搜尋關鍵字

四、Green 定理

Green 定理基本上是線積分與面積分之關係，實際上就是微積分基本定理的推廣。

Green 定理：
令 C 為平面上一分段平滑的封閉曲線而其所圍區域為 $\mathcal{R}$ ，假設函數 P(x,y), Q(x,y) 為連續且一次偏導數也連續則等式成立

$\begin{displaymath} \oint_c P dx + Qdy = \int \!\! \int_{\mathcal{R}} (\frac{\pa... ...partial y} \\ P & Q \end{array} \right\vert } dA \eqno{(9)} \end{displaymath}$

數學的角度：

由於曲線 C 的變化可大可小一般而言並沒有明顯的參數式，因此無法直接求線積分，然而我們可利用逼近 (approximation) 的概念來處理，這正是數學尤其是分析 (analysis) 的主要技巧。

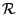
長方形 $\Longrightarrow{}$ 多邊形 $\Longrightarrow{}$ $\mathcal{R}$

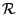I. $\mathcal{R}$ 為一長方形

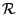$\mathcal{R}$ 之邊界 C = C₁ + C₂ + C₃ + C₄

$\begin{eqnarray*} C_1 : && a_0 \leq x \leq a_1 , y=b_0 \\ C_2 : && x = a_1 , b_... ...\leq x \leq a_1 , y=b_1 \\ C_4 : && x =a_0, b_0 \leq y \leq b_1 \end{eqnarray*}$

因此利用微積分基本定理可得

$\begin{eqnarray*} && \oint_C F \cdot d\overrightarrow{r} \\ &=& \oint_C P(x,y)d... ...ac {\partial Q}{\partial x} - \frac{\partial P}{\partial y})dxdy \end{eqnarray*}$

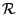II. 假設 $\mathcal{R}$ 可表為

$\begin{displaymath} \mathcal{R}= \{(x,y) \vert a \leq x \leq b, g_1(x) \leq y \leq g_2(x) \}, \; C = \partial\mathcal{R} \end{displaymath}$

我們分別處理 P(x,y) , Q(x,y)

$\begin{eqnarray*} && \oint_C P(x,y)dx \\ &=& \oint_{C_1} P(x,y)dx + \oint_{C_2}... ...a^b\int_{g_1(x)}^{g_2(x)} \frac{\partial P}{\partial y}(x,y)dydx \end{eqnarray*}$

同理可得

$\begin{displaymath} \oint_C Q(x,y)dy = \int_a^b \int _{g_1(x)}^{g_2(x)} \frac {\partial Q}{\partial x} dydx \end{displaymath}$

兩者合併

$\begin{eqnarray*} \oint_c P dx + Qdy &=& \int \!\! \int_{\mathcal{R}} (\frac{\pa... ...c{\partial}{\partial y} \\ P & Q \end{array} \right\vert } dA \end{eqnarray*}$

這就是 Green 定理，提供了我們關於線積分與面積分之關係，但這個逼近方法有個限制就是曲線 C 必須是有長度曲線 (rectifiable curve)，而且還要用到一致收斂 (uniformly convergent) 的概念。對於更一般的區域 Green 定理仍然是對的，但已經超過微積分的範圍，讀者有興趣可參考微分幾何方面的書。

例題 1：利用 Green 定理計算線積分

$\begin{displaymath} \oint_C (2xy-x^2)dx +(x+y^2)dy \end{displaymath}$

其中曲線 C 是由拋物線 y=x² 與直線 y=x 所圍區域之邊界。

解：要直接計算線積分勢必要將 C 化為參數式，然而利用 Green 定理取

$\begin{displaymath} P(x,y)=2xy-x^2 , \; Q(x,y)=x+y^2 \end{displaymath}$

則

$\begin{displaymath} \frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}=1-2x \end{displaymath}$

因此

$\begin{eqnarray*} \mbox{{\fontfamily{cwM0}\fontseries{m}\selectfont \char 159}\h... ...(1-2x) dA \\ &=&\int_0^1\int_{x^2}^x (1-2x)dydx = \frac{1}{30} \end{eqnarray*}$

Green 定理說明一封閉曲線 C 之線積分與 C 所圍區域之面積分（雙重積分）之關係，因此在特殊情形之下，線積分之幾何意義為「面積」；例如取

$\begin{displaymath} \frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y}= 1 \end{displaymath}$

則由 Green 定理知

$\begin{displaymath} \oint_C Pdx +Qdy = \int \!\! \int_{\mathcal{R}} 1 dA = \vert\mathcal{R}\vert \end{displaymath}$

通常可取 P,Q 如下：

$\begin{displaymath} \begin{array}{ll} P=0, & Q=x \\ P=-y, & Q=0 \\ P= -\frac{1}{2}, & Q=\frac{1}{2}x \end{array}\end{displaymath}$

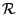系：區域 $\mathcal{R}$ 由分段平滑的封閉曲線 C 所圍成，其面積為：

$\begin{eqnarray*} \vert\mathcal{R}\vert &=& \frac{1}{2} \oint_C - ydx + xdy \\ &=& -\oint_C ydx = \oint xdy \qquad\qquad \eqno{(10)} \end{eqnarray*}$

: 例題2：試求橢圓 $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ 之面積。

解：將橢圓表為參數式

$\begin{displaymath} x=a \cos \theta ,\; y =b \sin \theta, \quad 0 \leq \theta \leq 2 \pi. \end{displaymath}$

利用系之結果得

$\begin{eqnarray*} A&=& \oint_C xdy \\ &= &\int_0^{2\pi} (a \cos \theta )(b \co... ... &= &\frac{1}{2}ab \int_0^{2\pi}(1+cos2 \theta)d \theta = \pi ab \end{eqnarray*}$

為著更深入討論 Green 定理，我們再計算一個例題並從其中得到靈感。

例題 3：已知 C 為任意封閉平滑曲線，試求線積分

$\begin{displaymath} \oint_{C} \frac{-ydx + x dy }{x^2 +y^2}, \qquad (0,0) \mbox{... ...1pt{\fontfamily{cwM1}\fontseries{m}\selectfont \char 107} } C. \end{displaymath}$

解：首先假設 (0,0) 並不包含在 C 之內部，則

$\begin{eqnarray*} && P(x,y)=\frac{-y}{x^2+y^2}, \quad Q=\frac{x}{x^2+y^2} \\ &... ...& \frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}=0 \end{eqnarray*}$

因此由 Green 定理知

$\begin{displaymath} \oint_{C} \frac{-ydx+xdy}{x^2+y^2} = \int \!\! \int_{\mathcal{R}} 0 dA =0 \end{displaymath}$

其次，若 (0,0) 在 C 之內部，此時 (0,0) 為一奇異點 (singularity)，克服這點的方法就是「避開它」，作一個半徑為 ρ，以 (0,0) 為圓心的圓 $B_{\rho}$ 考慮區域

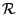$\begin{displaymath} \mathcal{R}'=\mathcal{R}- B_{\rho} , \; \partial \mathcal{R}'= C + \partial B_{\rho} \end{displaymath}$

由於 $\mathcal{R}$ 並不包含 (0,0)，因此利用前面的推論；

$\begin{displaymath} \oint_{\partial \mathcal{R}'} \frac{-ydx+xdy}{x^2+y^2}=0 \end{displaymath}$

但 $\partial\mathcal{R}' = C + \partial B_{\rho}$ ，故

$\begin{eqnarray*} \oint_C \frac{-ydx+xdy}{x^2+y^2} &=&\oint_{\partial B_\rho} \f... ...)^2+(\rho \sin\theta)^2} \\ &=&\int_0^{2\pi} 1 d \theta = 2 \pi \end{eqnarray*}$

註 1：此處積分值為 $2 \pi$ 表示曲線 C 繞了奇異點 (0,0) 一圈，而積分值等於 0 則是沒有繞到 (0,0)，這所對應的便是複變函數理論的繞數 (winding number)，在流體力學則是環流 (circulation)。

註 2：證明的過程中我們發現沿著曲線 C 之線積分等於沿著圓周 $\partial B_{\rho}$ 之線積分，這裡面的數學本質就是同倫理論 (homotopy theory)，因此 Green 定理可推廣到單連通區域 (simply connected region)，而這正是複變函數論研究的一重要主題，同時也說明複雜的曲線之線積分可化為簡單的曲線之線積分（例如圓周的線積分），這就是數學的精神──將複雜的問題化為簡單的問題。

註 3：若 C₁,C₂ 為任二條不相交的分段平滑封閉曲線而且都繞過原點 (0,0)，則

$\begin{displaymath} \oint_{C_1} \frac{-ydx+xdy}{x^2+y^2}=\oint_{C_2} \frac{-ydx+xdy}{x^2+y^2} \end{displaymath}$

這除了同倫理論之外，直接的意義就是該線積分對於形變 (deformation) 是一不變量。另外我們可透過極座標 (polar coordinate) 來看；令

$\begin{displaymath} \theta = \tan^{-1} \frac{y}{x} \end{displaymath}$

則被積分函數 (integrand) 成為

$\begin{displaymath} d \theta = \frac{-ydx+xdy}{x^2+y^2} \end{displaymath}$

因此這個線積分實際上就是在測量沿著曲線 C（逆時針方向）角度之變化量，當然若是繞了一圈則其變化量為 $2 \pi$ ，若是順時針方向繞了一圈則其變化量為 $-2\pi$ ，這個概念就是前面所說的繞數 (winding number)。

物理的角度：

Green 定理也可透過物理的角度來認識：令 $\mathcal{R}$ 為平面上的平滑曲線 C所圍之單連通區域，設 C 可表為 x=x(t), y=y(t) 之參數式，而向量

$\begin{displaymath} F(x,y)=(P(x,y),Q(x,y)) \eqno{(11)} \end{displaymath}$

表示流體的速度，我們想計算流體經過邊界 C 之通量 (flux)，仿照線積分將曲線 C 分為若干小段而看其中一段；首先是 x 分量通過 $\Delta s_i$ 之通量（斜線部分之面積）為

$P_i(x,y)\Delta s_i \cos \alpha_i$ ，其中 $\alpha_i$ 為朝外法向量 ν 與 x 軸之夾角，再將各部份全部加起來並利用 Riemann 和，知 x 軸部分之分量為

$\begin{displaymath} \oint_C P(x,y) \cos (\nu,x)ds \eqno{(12)} \end{displaymath}$

同理 y 軸之分量為

$\begin{displaymath} \oint_C Q(x,y) \cos (\nu,y) ds \eqno{(13)} \end{displaymath}$

因此全部之通量為

$\begin{eqnarray*} & &\oint_C[P(x,y) \cos(\nu,x) + Q(x,y) \cos (\nu,y)]ds \\ &=&... ...=&\oint_C F \cdot \nu ds , \; v=(\frac{dy}{ds},- \frac{dx}{ds}) \end{eqnarray*}$

另一方面我們看小矩形，由於由這矩形左側垂直邊上的流速為 P(x,y)，因此單位時間內有 $p(x,y)\Delta y$ 的水流入，而同一時間則約有 $p(x+\Delta x,y)\Delta y$ 的水流出，所以沿 x 軸方向之單位淨流量為

$\begin{displaymath} \frac{[P(x+\Delta x,y)-P(x,y)]\Delta y}{\Delta x \Delta y} \end{displaymath}$

令 $\Delta x \rightarrow 0$ ，得極限 $\frac{ \partial P}{ \partial x}$ 同理沿 y 軸之單位淨流量為 $\frac{ \partial Q}{ \partial y}$ 因此單位淨流量為 $\frac{ \partial P}{ \partial x} +\frac{ \partial Q}{ \partial y}$ 而通過整個區域 $\mathcal{R}$ 之全部通量為

$\begin{displaymath} \int \!\! \int_{\mathcal{R}} (\frac{ \partial P}{ \partial x} + \frac{ \partial Q}{ \partial y}) dxdy \eqno{(15)} \end{displaymath}$

因為水是不可壓縮（假設的），同一時間的水量必須從邊界 C 流出去（質量守恆），故

$\begin{displaymath} \oint_C Pdy-Qdx = \int \!\! \int_{\mathcal{R}} (\frac{ \par... ...\partial x} +\frac{ \partial Q}{ \partial y}) dxdy \eqno{(16)} \end{displaymath}$

這再次說明 Green 定理之物理意義為「守恆律」。

　1│2│3│4│5│6│7　


	（若有指正、疑問……，可以在此留言或寫信給我們。）

EpisteMath (c) 2000 中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有

編輯：朱安強 ∕ 繪圖：簡立欣

最後修改日期：4/26/2002