古希臘幾何三大問題 (第 4 頁)

　1│2│3│4│5　

古希臘幾何三大問題（第 4 頁）

康明昌

首頁 | 搜尋

．原載於數學傳播第八卷第二期、第八卷第三期分兩期刊出
．作者當時任教於台大數學系

‧註釋
‧對外搜尋關鍵字

4.超越數簡介

一個複數 x 叫做超越數(transcendental number) 的意思是說，對於任何 Q 上的多項式 f(T)，若 f(x)=0，則 $f(T)\equiv 0$ 。否則，就叫做代數數(algebraic numnbers)。

不難看出，x 是代數數的充分必要條件是 $[\mathbf{Q}(x):\mathbf{Q}]<\infty$ 。因為，若 [Q(x):Q]=n，則 1,x,…,xⁿ⁺¹，不可能在 Q 上線性獨立。所以可以找到不全為零的有理數 $\alpha_0$ , $\alpha_1$ ,…, $\alpha_n$ ，使得 $\alpha_0x^{n+1}+\alpha_1x^n+\cdots+\alpha_nx+\alpha_{n+1}=0$ 。所以 x 是代數數。

所有代數數形成的集合，變成一個體。（證明不是很容易，但是讀者值得自己做做看。） ⁵

如果 x 是超越數，則 Q(x) 的四則運算和有理函數

$\begin{displaymath} \mathbf{Q}(T) = \{ \frac{f(T)}{g(T)}:f(T), g(T) \mbox{{\font... ...0.1pt{\fontfamily{cwM1}\fontseries{m}\selectfont \char 31}} \} \end{displaymath}$

的四則運算完全一樣，例如 (1+x)(1-x)=1-x²。但是如果 x 是代數數，例如 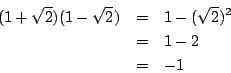$x=\sqrt{2}$ ，則

$\begin{eqnarray*} (1+\sqrt{2})(1-\sqrt{2})&=&1-(\sqrt{2})^2\\ &=&1-2\\ &=&-1 \end{eqnarray*}$

我們可以把 $x^2=(\sqrt{2})^2$ 繼續化簡。

超越數和無理數並不一樣。有理數是可以寫成 $\frac{q}{p}$ 型式的數，其中 p 與 q 是整數， $p\neq 0$ 。

$\begin{displaymath}\begin{eqalign} \mbox{{\fontfamily{cwM0}\fontseries{m}\select... ...tfamily{cwM1}\fontseries{m}\selectfont \char 98}} \end{eqalign}\end{displaymath}$

如 $\sqrt[3]{2}$ 是代數數， $\pi i$ 是超越數，i 是代數數而不是實數。

法國數學家 Joseph Liouville（1809～1882年）在1844年找出第一個超越數出來。Liouville 的方法是根據一個基本的概念：代數數是無法用有理數來高度逼近的。更精確的說，他證明

定理

若實數 ξ 是一個滿足

$\begin{displaymath} a_0\xi^n+a_1\xi^{n-1}+\cdots+a_{n-1}\xi+a_n=0 \end{displaymath}$

的代數數，a_i 是整數， $a_0\neq 0$ 。則必存在一個正數 K，使得 $\vert\xi-\frac{q}{p}\vert>\frac{K}{p^n}$ ，其中 $\frac{q}{p}$ 是足夠靠近 ξ 的有理數，且 $\frac{q}{p}\neq\xi$ 。

證明

設 f'(T) 是 f(T) 的導函數，其中

$\begin{displaymath} f(T)=a_0T^n+a_1T^{n-1}+\cdots+a_{n-1}T+a_n \; . \end{displaymath}$

找一個正數 M，使得只要 $\xi-1<u<\xi+1$ ，就會有 $\vert f'(u)\vert<\frac{1}{M}$ 。

若 $\frac{q}{p}$ 足夠靠近 ξ，使得

$\begin{displaymath} \xi-1<\frac{q}{p}<\xi+1 \; \mbox{{\fontfamily{cwM0}\fontseries{m}\selectfont \char 47}} \; f(\frac{q}{p})\neq 0 \end{displaymath}$

則

$\begin{displaymath} \vert f(\frac{q}{p})\vert=\frac{\vert a_0q^n+a_1q^{n-1}p+\cdots+a_{n-1}qp^{n-1}+a_np^n\vert}{p^n}\geq\frac{1}{p^n} \end{displaymath}$

又

$\begin{displaymath} f(\frac{q}{p})=f(\frac{q}{p})-f(\xi)=(\frac{q}{p}-\xi)\cdot f'(\xi) \end{displaymath}$

其中 $\xi-1<\xi_1<\xi+1$ ，故

$\begin{displaymath} \vert\xi-\frac{q}{p}\vert = \frac{\vert f(\frac{q}{p})\vert}{f'(\xi_1)} > \frac{M}{p^n} \end{displaymath}$

得證。

利用以上定理，Liouville 指出

$\begin{displaymath} \xi=0.110001000\cdots=\frac{1}{10}+\frac{1}{10^{2!}}+\frac{1}{10^{3!}}+\cdots+\frac{1}{10^{n!}}+\cdots \end{displaymath}$

是一個超越數。例如，假設 ξ 滿足一個57次的方程數，且 K=1000，那麼我們只要取一個有理數 η，η 是 ξ 的前57項的和，即

$\begin{displaymath} \eta=\frac{1}{10}+\frac{1}{10^{2!}}+\frac{1}{10^{3!}}+\cdots+\frac{1}{10^{57!}}=\frac{q}{10^{57!}} \end{displaymath}$

q 是某個整數。則

$\begin{displaymath} \vert\xi-\eta\vert=\frac{1}{10^{58!}}+\frac{1}{10^{59!}}+\cdots<2\frac{1}{10^{58!}}<\frac{1000}{(10^{57!})^{57}} \end{displaymath}$

因此 Liouville 定理不成立。故 ξ 不得不是超越數。

三十年以後，Georg Cantor 利用集合論的方法證明，所有的實數的代數數是可數的 (countable) 而實數是不可數的 (uncountable)，因此必有一個超越數存在。

1873年法國數學家 Charles Hermite（1822～1901年）證明

$\begin{displaymath} e \quad ( = \lim_{n\rightarrow\infty}(1+\frac{1}{n})^n) \end{displaymath}$

是超越數。

1882年 F. Lindemann 利用 Hermite 的想法，證明 π 是超越數。事實上 Lindemann 證明：若 $a\neq 0$ 是一個代數數，則 e^a 是一個超越數。取 a=1，得證 e 是超越數。取 $a=i\pi$ ，則 $e^{i\pi}=\cos\pi+i\sin\pi=1$ 不是超越數，故 $i\pi$ 不是代數數；得證 π 是超越數。

1900年 David Hilbert（1862～1943年）在巴黎的國際數學會提出有名的 Hilbert 的23個問題。他的第七個問題是：如果 a 與 b 都是代數數，且 $a\neq 0,1$ ，b 是無理數，則 a^b 是否為超越數？例如， $2^{\sqrt{2}}$ 、 $e^{-\pi}=e^{i\pi\cdot i}= (-1)^i$ 、 $e^{i\pi b}=(-1)^b$ 是不是超越數？

在1934年，俄國數學家 A.O. Gelfond 與德國數學家 T. Schneider 分別解決了 Hilbert 第七問題，答案是肯定的。

要證明某些數是超越數並不是很容易的。例如，0.123456789101112… 是不是超越數？（答案：是。）又如： $e+\pi$ 、e^e、 $\pi^{\pi}$ 、 $\pi^e$ 、 $2^{2^{\sqrt{2}}}$ 、 $2^{\pi}$ 、2^e、Euler 常數（= $\lim_{n\rightarrow\infty} (1+\frac{1}{2}+\cdots+\frac{1}{n}-\ln n)$ ）是不是超越數？事實上，到現在為止，我們連這些數是不是無理數都不知道。

由於超越數的研究，數學家連帶的研究，代數數的對數的線性組合估計值，整係數多頂式解的精確範圍，有理數逼近代數數的方式。同時數學家也設計出許多巧妙的方法來討論超越數。Hilbert 在提出第七問題時特別強調，要解決這個問題勢必發現許多新的方法與新的角度來瞭解無理數與超越數的本質。

有關 Lindemann 定理的證明，讀者可參考以下資料，

S. Lang,《Algebra》, Appendix, 492～499頁，這裏的證明是採用 Gelfond 與 Schneidel 方法。讀者只要具備複變函數的知識就可看懂。並且，就在這裏，Schanuel 猜測第一次出現在眾人眼前，Schanuel 猜測幾乎統攝超越數理論中許多主要的定理，如 Lindemann n 元素定理、Gelfond-Schneider 定理、Baker n 元素定理。可惜這個猜測到今天還沒有證明出來。

　1│2│3│4│5　


	（若有指正、疑問……，可以在此留言或寫信給我們。）

EpisteMath (c) 2000 中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有

編輯：黃信元

最後修改日期：5/3/2002