談談卜松過程 (Poisson Process) (第 6 頁)

　1│2│3│4│5│6　

談談卜松過程 (Poisson Process) （第 6 頁）

孫自健;石仲拓

．原載於數學傳播第二卷第四期
．作者當時任教於美國韋恩州立大學數學系;美國密西根大學數學系
‧對外搜尋關鍵字

附錄(C)

其實條件(iv")已經足夠推出條件(i),(ii),(iii),(iv)來，更清楚的一點說則是：假如 T₁, T₂,…,T_n,… 為獨立隨機變數，與有相同的指數分佈，參數為 λ ( $0<\lambda<\infty$ )。令

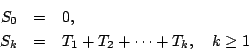
$\begin{eqnarray*} S_0 &=& 0 , \\ S_k &=& T_1 + T_2 + \cdots + T_k, \quad k \geq 1 \end{eqnarray*}$

又定義

$\begin{displaymath} X(t)=k, \quad \mbox{{\fontfamily{cwM1}\fontseries{m}\selectfont \char 231}} \quad S_k \leq t < S_{k+1} \end{displaymath}$

則 $\{ X(t), \, 0 \leq t < \infty \}$ 為一具有參數的卜松過程，即滿足(i),(ii),(iii),(iv)。

這項證明比較長，我們就省去不談。

　1│2│3│4│5│6　


	（若有指正、疑問……，可以在此留言或寫信給我們。）

EpisteMath (c) 2000 中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有

編輯：康明軒 ∕ 繪圖：簡立欣

最後修改日期：4/26/2002