���w����N�@�� t�AX(t) �O�b�ɶ� t �ɪ��@���H���ܼơA
�ڭ̴N�s�o�@���H���ܼ�
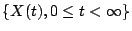 ���@���H���L�{
(random process��stochastic process)�C ���@���H���L�{
(random process��stochastic process)�C
-
- �w�q�@
���w�@���H���L�{
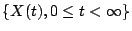 �����U�C������ɡA
�ڭ̴N�٥����@�ӤR�Q�L�{ (Poisson process)�A �����U�C������ɡA
�ڭ̴N�٥����@�ӤR�Q�L�{ (Poisson process)�A
- (i) X(0)=0
- (ii)������@�C�ɶ�
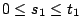
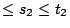 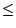 �K �K
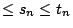 �An ���@���N��� �An ���@���N���
�O n �ӿW���H���ܼơC
- (iii)�����
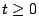 , ,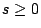 ,X(t)-X(0)�]=X(t)�^�M X(t+s)-X(s) ���ۦP�����v���G�C ,X(t)-X(0)�]=X(t)�^�M X(t+s)-X(s) ���ۦP�����v���G�C
- (iv)�����@�� t �M�@�� k
�䤤 �f �O�@���w���ѼơC
�ڭ̥��Τ@�ӹ�ҨӸ����o�DZ��N�q�C
���Q�ڭ̦b�@�������W�Y�I�[��q�L�o�I����q�q�C
�O X(t) ���q�ɶ� 0 ��ɶ� t �q�L�o�I���T���`�ơC
�h���� (i)���ܦb�ɶ� 0 �ɡA�q�L�����ƬO 0�C
����(ii)���b�����ۥ檺�ɬq (time intervals) ���q�L�����ƬO�ۤ��W�ߪ��C
����(iii)���u�n�ɬq���ۦP�A
���P�ɬq���q�L�����Ʀ��ۦP�����v���G�C
���� (iv) �� X(t) ���@�Ө㦳�Ѽ� 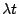 ���R�Q���G�C
���� (i) �O�X�z���C
�p�G�[������ɶ����Ӫ����ܡA
����(ii)�M (iii)�]�O�ܦX�z���C
����(iv)���G���I��M�A���O�b�ĤT�`�اڭ̱N�|�ͨ쥦�]�O�ܦX�z���A
�ӥB�@��������q�q�������]����o�@���w���C ���R�Q���G�C
���� (i) �O�X�z���C
�p�G�[������ɶ����Ӫ����ܡA
����(ii)�M (iii)�]�O�ܦX�z���C
����(iv)���G���I��M�A���O�b�ĤT�`�اڭ̱N�|�ͨ쥦�]�O�ܦX�z���A
�ӥB�@��������q�q�������]����o�@���w���C
��L�������Ҥl�A�p X(t) �N���b�ɬq [0,t]
���Y���]���`�@���i�Ӫ��q�ܦ��ơA�� X(t) �N���Y��|�b�ɬq
[0,t] ���ӱ������f�H�ӼƵ����A
���w���@�R�Q�L�{�A���P�ƹ�ܬ۪�C
�ҥH�R�Q�L�{�����ΫD�`���s�C
���R�Q�L�{�@��Ь���ؤ]�`�ĥΤU�����w�q�C
-
- �w�q�G
���p�@���H���L�{
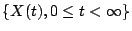 �����H�W������ (i),(ii),(iii) ��
�����H�W������ (i),(ii),(iii) ��
- (iv')
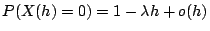 , ,
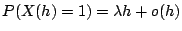 , ,
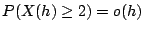 �C
�� h �ܤp�ɡA���a �f ���@�`�ơC �C
�� h �ܤp�ɡA���a �f ���@�`�ơC
�h�ڭ̺�
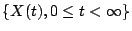 ���@�R�Q�L�{�C ���@�R�Q�L�{�C
�o�اڥΨ�Ÿ� f(t)=o(t) ���p
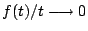 �A
�� t �A
�� t
 0 �C 0 �C
�H�U�ڭn�ҧY�b���� (i),(ii) �M (iii) ���U�A
���� (iv) �M (iv') �O�۵����A�ҥH�w�q�@�M�w�q�G�۵����C
���� (iv) 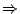 (iv')�G (iv')�G
����(iv)��
�ҥH�� k=0 �� 1 ��
��O
�ҥH�ڭ̱o�� (iv')�C
�A�� (iv') 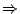 (iv): (iv):
�O
��O
�ҥH
�H�W�O���w 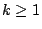 �C�p k=0 �W���]���ߡA���k��ĤG�����s�b�C �C�p k=0 �W���]���ߡA���k��ĤG�����s�b�C
�O
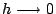 �o���{�� �o���{��
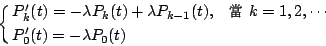 |
(4) |
��{�� (4) �q�`�s���캸���G���Ҥ�{�� (Kolmogorov equation)�C
����
 �o �o
�Ϊ�ȱ���
P0(0) = P(X(0)=0)=1�A�o�� c=1�A�ҥH
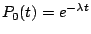 �C
�A�μƾ��k�Ǫk�A�� �C
�A�μƾ��k�Ǫk�A��
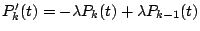 �A�`�N��ȱ���O �A�`�N��ȱ���O
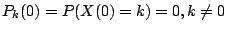 �A�h�i�o�� �A�h�i�o��
��O�ڭ̱o�����(iv)�C
|