談談卜松過程 (Poisson Process) (第 3 頁)

　1│2│3│4│5│6　

談談卜松過程 (Poisson Process) （第 3 頁）

孫自健;石仲拓

首頁 | 搜尋

．原載於數學傳播第二卷第四期
．作者當時任教於美國韋恩州立大學數學系;美國密西根大學數學系
‧對外搜尋關鍵字

三、

這一節裏，首先我們想談談為什麼在以上引的實例中，條件(iv)是合理的。我們已經證明在條件 (i),(ii) 和 (iii) 之下，條件 (iv)和 (iv')是相等的。條件(iv')說

$\begin{eqnarray*} P(X(h)=1) &=& \lambda h + o(h) \approx \lambda h, \\ P(X(h)\g... ...nus0.1pt{\fontfamily{cwM1}\fontseries{m}\selectfont \char 118} } \end{eqnarray*}$

用於車輛通過次數的例子，這個條件只不過說當時段 [0,t] 很短的時候，在時段 [0,t] 中通過一輛車的機率大概正是比於時段的長度 h，其比例常數就是 λ。另外這條件又說在時段 [0,h] 中，通過兩部車以上的機率幾乎是零。這樣的假定似乎是很接近現實的，那麼條件(iv)就不是太奇怪了。

第二節裏的證明 (iv')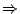 $\Rightarrow$ (iv) 牽涉到推演科爾莫果爾夫方程式和解這組微分方程式。下面我們準備用第一節的結果作一個不太嚴格但很直覺 (Intuitive) 的證明，讓你們更可以看出條件(iv)的合理性來了。

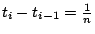假定(i),(ii),(iii)及(iv')成立。讓我們把時段 [0,t] 分成 n 等分， 0= t₀ < t₁ < t₂ < … < t_n = t， $t_i- t_{i-1} = \frac{1}{n}$ 。（如下圖所示）

條件 (ii) 說 X(t₁) - X(t₀), X(t₂) - X(t₁),…,… X(t_n) - X(t_n-1) 都是獨立的隨機變數，條件(iii)指出他們有同樣的隨機分佈，條件 (iv') 則說

$\begin{eqnarray*} && P(X(t_i)-X(t_{i-1})=0) \approx 1 - \lambda (t_i -t_{i-1}) =... ... \lambda \frac{t}{n} \\ && P(X(t_i)-X(t_{i-1})\geq 2) \approx 0 \end{eqnarray*}$

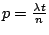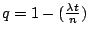所以每個獨立隨機變數 X(t_i) - X(t_i-1) 都幾乎是一個銅板模型 (Coin model)，正面（即等於 1）的機率是 $p = \frac{\lambda t}{n}$ ，反面（即等於 0）的機率是 $q = 1- (\frac{\lambda t}{n})$ 。所以這 n 個隨機變數的和。即總共正面出現的次數為

$\begin{displaymath} X(t) = [ X(t_n) - X(t_{n-1})] + [X(t_{n-1}) - X(t_{n-2})] +\cdots + [ X(t_1) - X(t_0)] \end{displaymath}$

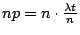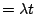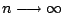（幾乎是有一個二項分佈，這裏 $np = n \cdot \frac{\lambda t}{n}$ $= \lambda t$ 。令 $n \longrightarrow \infty$ ，用第一節的結果，對任一 k=0,1,2,…

$\begin{displaymath} P(X(t)=k) \approx {n \choose k}p^kq^{n-k} \longrightarrow \frac{(\lambda t)^k}{k!} e^{-\lambda t} \end{displaymath}$

所以 X(t) 有一個具有參數 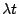$\lambda t$ 的卜松分佈，這正是上面的條件(iv)。這個證明不夠嚴格，可是比第二節的證明容易了解，假如你能了解這個證明，你就明白為什麼條件(iv)並不是很突然的了。

卜松過程有一個很有用的特性，再拿車輛次數的例子來說。如果我們用 T₁ 表示從時間 0 到第一輛車通過這一點時的時段，用 T₂ 表示從第一輛車通過這點到第二輛車通過這點的時段，……等等。則 T₁, T₂, T₃,… 都是隨機變數。我們叫它們做「等候時間」(waiting time)。假定條件(i),(ii),(iii)和(iv)成立，即假設在 [0,t] 間通過的車數 X(t) 為一卜松過程，則我們可以證明
(iv") T₁, T₂, T₃,… 都是獨立的和具有相同分佈的隨機變數，其共同的機率分佈是

$\begin{displaymath} P(T \leq t) = 1 - e^{-\lambda t} , \quad t>0 \end{displaymath}$

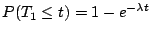即一指數分佈，其參數為 λ。要證明 $P(T_1 \leq t) = 1 - e^{-\lambda t}$ 非常容易，因為

$\begin{eqnarray*} P(T \leq t) &=& 1-P(T_1>t) \\ &=& 1-P(X(t)=0) = 1 - e^{-\lambda t} , \quad t>0 \end{eqnarray*}$

可是其他的部份，如證明 T₁, T₂,… 是獨立的，和 T₂, T₃,… 都有像 T₁ 一樣的分佈等等，有興趣的讀者請參考附錄 B。其實從條件(i),(ii),(iii)和(iv") 也可以推出(iv)或(iv')來。所以這也是卜松過程的另一種定義。其證明並不太難，先用 T₁, T₂,… 在條件(iv")中的性質，計算

$\begin{eqnarray*} &&P(T_1+T_2+\cdots+T_k \leq t) \\ &=& \lambda^k \int \cdots \... ... t_1} e^{-\lambda t_2} \cdots e^{-\lambda t_k} dt_1 \cdots dt_k, \end{eqnarray*}$

再由關係

$\begin{eqnarray*} && P(X(t)=k) \\ &=& P(T_1+T_2+\cdots+ T_k \leq t, (T_1 +T_2 +... ...2+\cdots+ T_k \leq t) - P(T_1 +T_2 + \cdots T_k+T_{k+1} \leq t ) \end{eqnarray*}$

計算出機率 P(X(t)=k) 來。讀者可自己計算一下，或參看教科書，有興趣的可再讀附錄C。

此地我們只想指出卜松過程是一種計數過程 (counting process)，因 X(t) 都是取整數值的。其平均值 (mean)

$\begin{eqnarray*} EX(t) &=& \sum^\infty_{k=0} k \frac{(\lambda t)^k}{k!} e^{-\la... ...\\ &=& \sum^\infty_{k=0} \frac{(\lambda t)^k}{k!} = \lambda t, \end{eqnarray*}$

所以 λ 代表的意思是單位時間內通過車輛數次的平均值。

如果反過來我們從條件(iv")來看 T₁, T₂,…。代表前後車之間的等候時間，他們的平均值

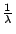$\begin{displaymath} ET = \int^{\infty}_0 (\lambda e^{-\lambda t}) dt = \frac{1}{\lambda} \end{displaymath}$

所以 $\frac{1}{\lambda}$ ，代表前後兩車通過時間差的平均值。

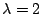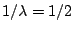譬如說 $\lambda=2$ ，而 t 是用分鐘表示，用計數的觀念每分鐘平均有兩車通過，如果用等候時間的觀念來想由於 $1/\lambda = 1/2$ ，所以平均每 1/2 分鐘有一車通過，這兩種觀念豈不配合得很好，也正是卜松過程的一種兩面性。

卜松過程還有一種定義，其牽涉到的證明比較麻煩，我們把它放在下面的附錄A裏。

　1│2│3│4│5│6　


	（若有指正、疑問……，可以在此留言或寫信給我們。）

EpisteMath (c) 2000 中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有

編輯：康明軒 ∕ 繪圖：簡立欣

最後修改日期：4/26/2002