| |
第二個例子令
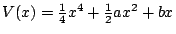 ，則
V'(x)=x3+ax+b，V''(x)=3x2+a。仍先考慮
V'(x)=x3+ax+b=0，這個三次方程式有三個根，其中一定有一個實根 α，另外兩個根或為共軛複數，或為重根，或為相異實根，就要取決於三次方程式的判別式
4a3+27b2
大於 0，等於 0 或小於 0 了。其實上面的判別式很容易由重根考慮而得：V'(x)=0 若有重根 x，則 x 必須滿足
[V'(x)]' = V''(x)=0。因此解方程組
消去 x 而得 a=-3x2，
b=-x3+3x3=2x3，故
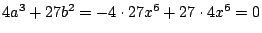 ，因此在圖三中，(a,b) 平面的尖點曲線 B:4a3+27b2=0上，V'(x)=0有重根。尖點曲線的內側 A 中隨便取一點，例如 a=-1,b=0，這時判別式
4a3+27b2=-4<0，而且
V'(x)=x3-x=x(x2-1)=0
故，x=0, 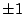 為三個實根。因為判別式是 a,b 的連續函數，所以在 A 的部分判別式之值為負。因此若有一點 (a,b) 落在 A 中，則這時
V'(x)=x3+ax+b=0 有三個實根。特別當 x 趨向正、負無窮大時，V(x) 之值都趨向正無窮大，可見 V(x) 之圖形大概就像圖四中所畫的曲線，它具有兩個極小以及一個極大，分別以 x1, x3 以及 x2 表示之。取尖點曲線 B 之外側的一點 (a,b)，例如a=0,b=-1，則這時判別式
4a3+27b2=27>0，而且
V'(x)=x3-1=(x-1)(x2+x+1)=0，故 x=1,
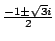 為一個實根及兩個共軛複數根。可見在 B 的外側只有一個實根，而當 x 趨近於正、負無窮大時，V(x) 之值仍都趨向正無窮大，因此V(x)之圖形大概就像圖五中所畫的單單具有一個極小 x1 的曲線。
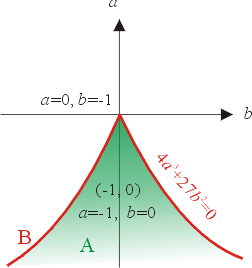
圖三
|
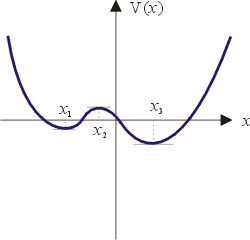
圖四
|
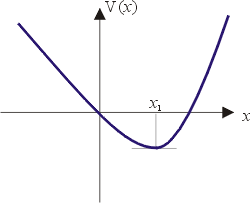
圖五
|
利用這種結果我們可以很容易畫出 V'(x)=0 之圖形。它是一個覆蓋在 (a,b) 這平面上的曲面 M，在 B 外側 M 只為單層，因為只有一個實根，但是在 B 的內側（即 A 的部分）M 卻有三層，因為我們已知這時 V'(x)=0 有三個實根。我們能證明這三個實根必需是相異實根。若不然，設有兩根同為實數 h，另一根為實數 k，則比較下式兩邊之係數:
V'(x)=(x-h)2(x-k)=x3+ax+b
可得：k=-2h,
a=h2+2hk=-3h2,b=-h2k=2h3，因此這時判別式
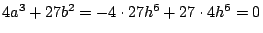 。這表示點 (a,b) 在曲線 B 上，跟點 (a,b) 落在 B 之內側的假設不符。
當 (a,b) 為原點 O 時，V'(x)=x3=0 之三個根皆為 0，因此 M 為經過 (a,b) 平面之原點的曲面，但是通常的習慣是把 M 往上平移到適當的位置，以便清楚畫出 M 跟 (a,b) 平面的關係，就如同圖六中使用 P 點代表 O 點。M 在 P 點附近打了兩摺，先是從圖六中左邊的上層，以 P 點為界，沿B'1往左下方摺疊出圖中畫為中層的部分，然後再一次以 P 點為界，沿 B'2
往右下方摺疊成下層。令 B1,B2 分別為 B'1 及 B'2 在控制平面（即 (a,b) 平面）上的投影，則 B1 跟 B2 加上原點 O 一起合成圖三中的尖點曲線 B。在 A 的部分，同時被上、中、下三層覆蓋，上下兩層各代表極小，中層代表極大，這三個 x 值正是 V'(x)=0 的三個實根。圖六中我們還特別畫出一條穿過 A 部分的一點，且平行於 x 軸的直線。這直線交 M 於 x1,x2,x3 三點分居下、中、上三層，這是對應到圖四中的三點。同樣我們也可考慮經過B之外側任意點的垂直線，則這直線只交 M 於一點 x1，正是對應到圖五中的情形。但是這時我們最好注意下列的差別：當 a 值為負時，若點 (a,b) 在 B2 之外側，則只有上層覆蓋於其上，但是若點 (a,b) 在 B1 之外側則只有下層覆蓋於其上。當 a 值為正時，則上下層連成一片，不分上下，而代表V'(x)=0唯一的實根，也是V(x)的極小。
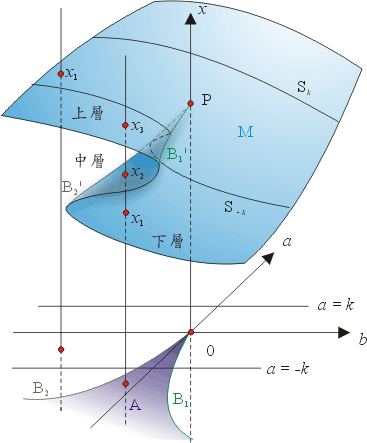
圖六
|
當a為固定正數k時，考慮一個a=k（b,x隨意）而平行(b,x)這坐標面的平面。這平面交(a,b)坐標面於直線a=k（b隨意，x=0），而交M於一條簡單的曲線Sk。如圖六、圖七所示。從Sk投射到直線a=k是一對一的映射，即Sk中不同點一定投射到a=k中之不同點。但是如果考慮a為固定負數-k時，則平行於(b,x)這坐標面的平面交(a,b)平面於直線a=-k,但卻交M於曲線S-k，（看圖六及圖八）這時S-k到a=-k之投射並非一對一。在a=-k直線上有一個由尖點曲線所夾出的線段[B2,B1]，在這線段上都有S-k上的三點投射下來。但是投射到B1點的卻只有兩點，原因是當b值在A中向B1趨近時，分居上中兩層之兩點（一個極小，一個極大）愈來愈接近，終於當b值是B1時相疊成一點G1，可見S-k在G1點的切線是平行於x軸的;換言之，S-k是個可微分的曲線，它對x的微分（此即V''(x)）在G1點為O。在B2點上方的情形也完全類似:中層的極大與下層的極小碰撞而合成一點G2，而V''(x)在這點之值亦為0，G1,G2正表示重根。
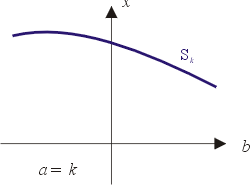
圖七
|
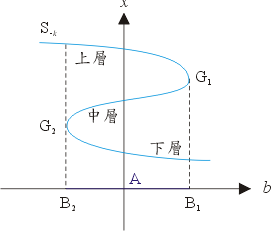
圖八
|
如果所考慮的多項式改用為
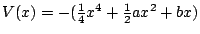 ，與原來的V(x)相差一個符號，則上面所有的討論可以完全同樣再講一次，而只需把圖四、圖五上下顛倒過來，又把所有極大改成極小，極小改成極大就成了。圖三、圖六、七、八的形狀都不變，因為所處理的是
V'(x)=-(x3+ax+b)=0，正好跟前面處理的x3+ax+b=0完全相同，只需叫上、下層代表極大，中層代表極小就可。
圖六中所畫的數學模型通常就叫做尖點劇變（cusp catastrophe）模型，集合B是由V'(x)=0及V''(x)=0之解投射下來的，通常稱為分歧點集（bifurcation set）。B中所包含的B1及B2中之點其實就該點附近而言，都只是摺點，它代表一個極小打摺到極大來。但是原點O卻是個新型態的奇異點，在這點附近M同時打了兩摺。
|
|
|
