重複逼近面面觀

　1│2│3│4│5　

首頁 | 搜尋

．原載於科學月刊第二卷第六期

‧註釋

重複逼近面面觀
兼介向量變換

林孝信

I
II
III、矩陣代數淺介
IV
V

在本期〈我們自己做計算機〉一文的第九章中，提到重複逼近法 (Iterative Process) 解聯立一次方程式。原文未詳細說明。這是個應用廣泛、理論本身又十分有趣的問題，因此在此略作說明。

從初中起，我們就學過解一次聯立方程式，而且我們知道日常生活見到的許多四則計算問題，多數都屬聯立方程式的問題。事實上一次聯立方程式應用的範圍更要廣得多，許多高深的物理、化學或工程的研究，隨時都會用到這些粗淺的計算。所以這個基本的運算，必須要徹底了解它，要從各個角度了解它。

以下我們以重複逼近法為主題，環繞它作各種討論分析。

先研究最簡單的二元一次聯立方程式：

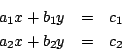
$\begin{eqnarray*} a_1 x+b_1 y &=& c_1 \\ a_2 x+b_2 y &=& c_2 \end{eqnarray*}$

基本解法是二式各乘上適當係數，相減以消去未知數之一（x₁ 或 x₂），結果是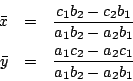

$\begin{eqnarray*} \bar{x} &=& \frac{c_1 b_2-c_2 b_1}{a_1 b_2-a_2 b_1} \\ \bar{y} &=& \frac{a_1 c_2-a_2 c_1}{a_1 b_2-a_2 b_1} \end{eqnarray*}$

這樣的計算，人人會算，人人易算。電子計算機當然也會算，但卻未必「易」算──尤其當多元（譬如說二十元）聯立時。當然，二十元聯立方程組，也不是人人「易」算。通常每個未知數也是個分數

$\begin{displaymath} x_1=\frac{\triangle_1}{\triangle} \end{displaymath}$

但此時分子分母各為 20！（即 $20 \times 19 \times 18 \times \cdots \times 3 \time 2 \times 1$ ）那麼多個數字相加減而來；而每個數字又分別由20個不同係數相乘得出的。這些加減乘除雖難不倒計算機；但我們要命令（寫程式(Program) ^編註）可就十分複雜了。

這時我們就想起計算機的特點了──「快」。利用此一特點，我們能不能想個法子使計算不必完全準確，但程式（命令）變得十分簡單；再利用計算機重複多算幾次，便可求出足夠精確結果？這正是重複逼近法的精神。

那麼，怎樣的計算，會使程式簡單？例如，

a₁ x= c₁

的計算，程序很簡單，只要把係數 a₁ 除過去便得了。但如

a₁ x+b₁ y=c₁

便不簡單。因為 y 的值不曉得（假設先要解 x），我們只好和下一個方程式聯立，一旦聯立，公式便複雜了。倘若我們假定 y 為某一定值 y₀，那麼便可輕易求出 x=x₁。當然，此時 x₁ 不是真正的解，因為 y₀ 是「假定」的。把這個 x₁ 值代入第二方程式

a₂ x+b₂ y=c₂

便很容易也求出 y=y₁。（這個當然也不精確。）

但現在 y₁ 比 y₀ 好些，不完全憑空「假定」，而是經過一番計算得來（雖然計算根源，還是假定了 y₀）。現在把 y₁ 代入第一式子，又可算出 x=x₂，這個 x₂ 跟方程組的關係，就比 x₁ 要深了一層。把 x₂ 代入第二式，又得到 y₂；然後又代回第一式得 x₂……如此循環不已，這就是重複逼近法。

這方法的命令（程式）非常簡單，而且可以一樣容易地推廣到20……甚至100元聯立方程式。只需計算夠快，可以連續多算幾次，便可利用此法。因此它在電子計算機中常被採用。

可是妳是不是覺得有點不太保險？對啦！我們怎知這樣算下去，會「逼近」我們要求的真正答案？說不定愈離愈遠呢！x₂ 只比 x₁ 關係深，但「關係深」不一近「逼近」答案，而且，最初我們要「假定」y₀ 為多少？它和「逼近」有沒有關係？

這話不錯！我們就進一步算算看。現在倘若我們已算了 n 次，把 y_n 代入第一式：

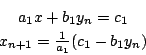
$\begin{eqnarray*} & a_1 x+b_1 y_n=c_1 & \\ & x_{n+1}=\frac{1}{a_1}(c_1-b_1 y_n) & \end{eqnarray*}$

再代 x_n+1 入第二式得 y_n+1：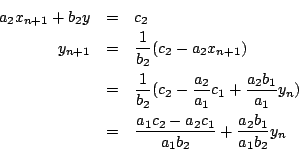

$\begin{eqnarray*} a_2 x_{n+1}+b_2 y &=& c_2\\ y_{n+1} &=& \frac{1}{b_2}(c_2-a_2... ... &=& \frac{a_1 c_2-a_2 c_1}{a_1 b_2}+\frac{a_2 b_1}{a_1 b_2} y_n \end{eqnarray*}$

我們要看看，y_n+1 和 y_n 那個比較靠近真正的解 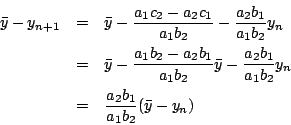$\bar{y}$ （ $=\frac{a_1 c_2-a_2 c_1}{a_1b_2-a_2b_1}$ ）。我們看 $\bar{y}$ 和 y_n+1 差多少？

$\begin{eqnarray*} \bar{y}-y_{n+1}&=&\bar{y}-\frac{a_1 c_2-a_2 c_1}{a_1 b_2}-\fra... ...{a_2 b_1}{a_1 b_2}y_n\\ &=&\frac{a_2 b_1}{a_1 b_2}(\bar{y}-y_n) \end{eqnarray*}$

這是個十分漂亮的結果！我們發現，只要 $\frac{a_2 b_1}{a_1 b_2}$ 的絕對值小於 1，即 |a₂ b₁|<|a₁ b₂|，那麼 y_n+l 就比 y_n 更趨近真正的值 $\bar{y}$ 。

從另個角度來看， $\frac{a_2 b_1}{a_1 b_2}$ 與 n 無關。這就是說， $\bar{y}-y_n$ 與 $\bar{y}-y_{n-1}$ 之比也是 $\frac{a_2 b_1}{a_1 b_1}$ 。因此，把

$\begin{displaymath} \bar{y}-y_n=\frac{a_2 b_1}{a_1 b_2}(\bar{y}-y_{n-1}) \end{displaymath}$

代入上式，再把

$\begin{displaymath} \bar{y}-y_{n-1}=\frac{a_2 b_1}{a_1 b_2}(\bar{y}-y_{n-2}) \end{displaymath}$

又代入。如此不斷代入，直到 y_n-n=y₀ 為止，我們就得：

$\begin{displaymath} \bar{y}-y_n=(\frac{a_2 b_1}{a_1 b_2})^n (\bar{y}-y_0) \end{displaymath}$

只要 $\vert\frac{a_2 b_1}{a_1 b_2} < 1\vert$ ，當 n 夠大時， $\bar{y}-y_n$ 便可稱心如意地「小」。

因此得到結論：

1. y_n 不一定愈來愈靠近 $\bar{y}$ 。

2. 但我們一定可辦到這點──如果 $\left\vert \matrix{ a_2 & b_1 \cr a_1 & b_2 \cr } \right\vert >1$ 那麼只需將兩個方程式對調一下。

3. 是否愈來愈「逼近」，和 y₀「假定」為什麼值無關。但要具體算出 y_n 和 $\bar{y}$ 的差別時，y₀ 就有影響了。

以上是對 y₀ 的計算。對 x_n 的結果完全一樣，比值亦為 $\frac{a_2 b_1}{a_1 b_2}$ （不是 $\frac{a_1 b_2}{a_2 b_1}$ ！萬一是如此，就天下大亂了！）詳細計算請讀者自己來。

對外搜尋關鍵字：
．線性組合

　1│2│3│4│5　


	（若有指正、疑問……，可以在此留言或寫信給我們。）

EpisteMath (c) 2000 中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有

繪圖：簡立欣

最後修改日期：4/29/2002