我們已能算出 A-1 具體的運算還要借用行列式的性質:行列式有兩行或兩列相等,則為零。因此,如在三度空間,把一個行式某一行的元素換以第二或第三行,其值為零。如此,我們可以找出一個向量和兩個向量垂直(內積為零),而和第三個內積為 1。(這是三度空間情形,高度空間可依此類推。)這是要點。細節請讀者自行補上。
因此我們可解聯立方程:
其解為
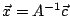 。 。
如何將這新工具應用到本文開頭所討論的重複逼近法呢?且再重新看看重複逼近法是怎回事。
以三元一次聯立方程式為例:
或
 , ,
假設已求了 n 次,故在第一式中,A12 的 x2 及 A13 的 x3 是代入上次求得的 xn2,xn3,便可求出 xn+11;第二式中 A23 的 x3 還用 xn3,但 A21 的 x1 改用剛求得的 xn+l1 代入;如此求出 xn+12。把 xn+11、xn+l2 代入第三式,便得 xn+13。換言之,可寫成:
或
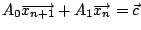 ,其中 ,其中
故
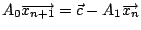 ,所以 ,所以
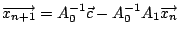 。
但,同理, 。
但,同理,
將各式逐次往上代入,則得:
式中,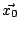 是「假定」的,「猜」的。 是「假定」的,「猜」的。
我們要知道的,是當重複算很多次後(n 愈來愈大),
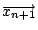 會不會逼近所要求的解答 會不會逼近所要求的解答 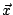 ? ?
顯然,如果
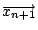 要趨近於真正解答 要趨近於真正解答 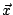 ,那麼含有用「猜」的右邊第二項 ,那麼含有用「猜」的右邊第二項
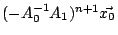 應趨近於 0,而另外一項應趨近於 應趨近於 0,而另外一項應趨近於 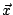 。也就是說: 。也就是說:
什麼狀況下,這兩個條件可以成立呢?顯然,如果 (-A0-1A1) 這個變換把任一個向量變得較小,如此一再重複地變換下去,最後終會把一個向量縮成零向量,即
同樣,如果 (-A0-1 A1) 把一個向量變小,那麼我們可以證明上二式子一定成立(證明的過程,和無窮等比級數的求和法類似,請參看初中代數課本。)
當然,(-A0-1 A1) 未必會把一個向量長度變得較小。這就需要把聯立方程組的程序作適當調整。但經過適當調整後,一定可達到我們的要求。讀者試以三元,四元等聯立方程式為例,實際安排算之。
|