如何求反變換 A-1 呢?
首先,根據定義,對任何向量 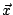 , ,
但一個向量 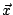 也可看做被一個單位變換 I 所作用。所謂單位變換就是把每個向量保留在原來地位,就好比任何數被 1 乘其值不變。換言之,單位變換就是不變換: 也可看做被一個單位變換 I 所作用。所謂單位變換就是把每個向量保留在原來地位,就好比任何數被 1 乘其值不變。換言之,單位變換就是不變換:
如寫成矩陣則是(三度空間為例)
即矩陣上,從左上角向右下角的主對角線各元素為 1,其他為 0。
因此,對任何的 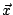 , ,
便得 A-1A=I。
有了這個公式,便可求反變換了。這是個關鍵。
再進一步想想變換的意義。變換是把一個向量變成另個向量。
向量兼具大小與方向,因此一個變換也可從大小與方向二部分來考慮。
先說大小:怎樣衡量一個變換的大小呢?當然是看各個向量經變換後,
新向量的大小和原向量大小來比較。但向量無窮多個,我們以哪幾個作標準呢?
最簡單而切中要害的選擇,是考慮各坐標軸上的單位向量。
因為所有其他向量都可以表以這些單位向量倍數的代數和
(叫做線性組合 Linear Combination)。在三度空間的例子中,這三個單位向量分別為:
經過 A 變換後,分別變成:
變換出的三個新向量,剛好是變換矩陣的三列數字!顯然放大率應由變換矩陣的九個數字來決定。
我們當然可算出這三個新向量的長度,原來單位向量的長度為 1,故新向量的長度即表出了變換的放大率。問題是拿那一個長度當代表?或者把三個長度加起來?乘起來?拿一個當代表是以偏概全;把三個長度籠統地加、乘起來則缺乏方向性。譬如前兩個新向量剛好一樣(即
A11=A12, A21=A22, A31=A32),從向量空間看來,原來的兩個單位向量是個正方形的兩邊,變換後兩個向量重合為一個,於是把一個正方形變換為一條線段。這時放大率(的絕對值)應當最小(事實上等於零)。但如用三個長度相加或相乘,便表現不出來。毛病出在對變換後新向量的方向性缺乏適當考慮。
從上述討論,我們發現合理的放大率應該用變換後新向量所圍成平行四邊形的面積(二度空間),或平行六面體的體積(三度空間)等等來表示。這體積如何算出?它是變換矩陣 A 的行列式。以三度空間為例,它是
因此,行列式代表一個變換矩陣的大小,(就好比絕對值表複數的大小)。行列式和變換矩陣有不可分離的關係,要介紹行列式,最順其自然的方法是從矩陣著手。(猶憶以前該高中課本行列式的介紹,從一些逆序,定義,十大性質等之著手,搞了一大堆定理、難題和解題技巧,卻不知行列式是幹什麼用的。)
有兩個問題未解決:
-
- 1.
怎知行列式
代表由
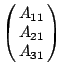 ,
,
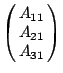 及
及
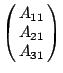 三個向量所圍成平行多面體的體積?
三個向量所圍成平行多面體的體積?
- 2.
用體積代表變換率(大小)會不會產生任何矛盾?(例如前面提過用三個長度相加,乘便有矛盾。)
這兩個問題不是三言兩語可以說完。且作為一項挑戰、請讀者研究,把心得寄來本刊。以上是變換的大小。
至於變換的方向,行列式事實上也表達了一部分。例如兩個向量對調,
行列式便變號(行列式兩行或列互換,則變號)。變換方向性的詳細情形,
不擬多費篇幅,也請讀者自行試試看。(按方向性可分三類:各個新向量彼此是否保待互相垂直?各個新向量彼此的次序是否更調了?是否把某方向的向量變成負向量?可由此線索出發研究。)
方向性中,垂直關係對於求反變換 A-1 很重要。先談如何表示兩個向量是否互相垂直。我們當然可以用兩個向量的夾角來表示,夾角 90°便是互相垂直。但一個更基本的概念是投影──從一個向量投影到另一個向量。當兩個向量互相垂直時,投影的長度為零;互相平行時,「影子」最長。因此我們可以用投影的長度來表示兩個向量夾角的大小,(見圖III-1)。但是我們算 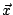 在 在 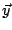 上的投影 xy 呢?還是拿 上的投影 xy 呢?還是拿 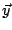 在 在 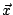 上的投影 yx 作標準呢?二者都顧此失彼。解決之道,是將 xy 乘以 上的投影 yx 作標準呢?二者都顧此失彼。解決之道,是將 xy 乘以 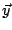 向量本身的長度 |y|(這剛好是 向量本身的長度 |y|(這剛好是 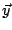 向量本身的投影長度)。由平面幾何,我們很容易證出 向量本身的投影長度)。由平面幾何,我們很容易證出
這樣的乘積叫做 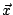 和 和 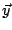 的內積 (Inner product)。
倘若 的內積 (Inner product)。
倘若 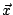 剛好在 X 軸上,長度為 x1,則可以寫作(假定在二度空間): 剛好在 X 軸上,長度為 x1,則可以寫作(假定在二度空間):
若 y 向量
則在 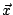 向量的投影為: 向量的投影為:
(見圖 III-2)若 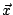 向量在 Y-軸上,長度為 x2,則 向量在 Y-軸上,長度為 x2,則
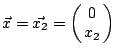 , yx=y2,
故 , yx=y2,
故
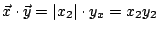 。現在假設 。現在假設 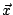 不剛好在坐標軸上,其一般形式可寫成: 不剛好在坐標軸上,其一般形式可寫成:
用一些平面幾何知識,讀者可自行證出:
故
這是個重要式子。我們發現,借用投影的觀念,可以從分向量的大小直接寫出內積。我們要知道兩個向量是否垂直,只須算算他們的內積是否為零。(內積還有更多用途。例如它可表示一個向量 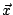 的長度 |x|: 的長度 |x|:
只需求向量和他本身的內積便得了。)有了內積,便可回過頭來求反變換 A-1 了。
前面提過,反變換 A-1 和原變換的關係是(假定二度空間):
這兒涉及兩個變換(或矩陣)的相乘(A 與 A-1 相乘)。它代表兩個變換的綜合變換。因為我們要實際算出 A-1 矩陣的各個元素,所以得先知道矩陣乘積 AB=C 這個新矩陣元素為多少?且從變換原來意義說起:
另方面,AB=C。即
所以,比較上二式子,
亦即
的乘法為 A 的一列各元素分別乘 B 一行的各元素。如果把
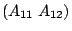 及 及
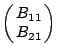 看成兩個向量,(前一個向量叫列向量,次一個叫行向量),矩陣的乘積便相當於求他們的內積!
因此,
看成兩個向量,(前一個向量叫列向量,次一個叫行向量),矩陣的乘積便相當於求他們的內積!
因此,
這個式子等於說,反變換 A-1 是由一些列向量組成,第一個列向量
(A11-1, A12-1, A13-1) 和原變換的所有行向量都互相垂直(內積為 0),除了第一個
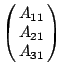 ,其內積為 1。A-1 的第二個列向量亦與 A 的每個行向量相垂直,除了第二個以外。以下依此類推。
,其內積為 1。A-1 的第二個列向量亦與 A 的每個行向量相垂直,除了第二個以外。以下依此類推。
簡言之,反變換是求一組列向量,這些列向量和原變換的行向量組只差一個不垂直;不垂直的內積為 1。
這種奇妙的關係用途卻很廣。除了求反矩陣,解聯立方程組外,也應用在固態物理結晶學上。在那兒,我們常用一組向量來表示晶體的格子組織;如把這組向量湊成一個變換,反變換的向量組便是晶體學上常用的 Bravais 向量,是研究晶體學或固態物理不可或缺的工具。
|