阿林談微積分

　1│2│3　

首頁 | 搜尋

．原載於科學月刊第一卷第四、六、七期，分三期刊出
．作者當時任教於台大數學系

阿林談微積分

曹亮吉

上篇
中篇
下篇

上篇

下了車，小華繃著慘白的臉：「這是什麼鬼路！彎彎曲曲的，車子轉來轉去，身子就跟看左搖右幌。又是一下子走，一下子停，把人搞得前仰後合的。唉呀！我差一點就吐出來了。」

「不對，不對，什麼前仰後合的，應該是後合前仰才對。」小明嘻嘻哈哈地說著，他是最不會暈車的。

「你說什麼?這又有什麼不同？」

「不同，不同，當然不同！車子一開動，人應該往後倒，車子一停，人應該往前倒。所以應該是後合前仰才對。」

「貧嘴。」小華嘟著嘴，無可奈何地說。

阿林看到小明嚥了一口水，一付又要說話的樣子，忙看打圓場：「好了，好了。今天是出來郊遊的。再吵下去，興緻就給你們弄光了。快走吧！」

轉過一段公路，登上了蜿挺的山徑，走了一個鐘頭。只見一塊巨石從茅草中突出。阿林說:「我們爬上去休息。這就是我說的「觀景石」。」

好不容易才把小華拉上那塊石頭。只見丈高茅草從身旁一直延伸到山腳，細長的公路成了界線。過了公路，則是一畦畦的稻田，綠油油地，一直漫延到對面的山腳邊。小華拍手叫著：「天氣好好哦！那邊一塊一塊的稻田都看得清清楚楚。綠油油的一片，今年一定豐收。」

「你懂得什麼！怎麼知道一定豐收？你連那裏有多少塊稻田都搞不清楚。」小明挑戰著。

「那還不簡單。橫的這邊有六塊，直的那邊有四塊。唔！不對，三塊。第四塊並不全。」（如圖一）

圖一

「不全也要算呀！難道非得四四方方的才算是稻田？」

「那怎麼算？有的是半塊不到，有的大到快成一整塊，還有第五排，大部份的恐怕連四分之一塊都不到呢！你說怎麼算？」

「用微積分可以算出來！」

「怎麼算？」

小明無助了，望著阿林。昨天阿林拉著他，硬要把微積分的神妙告訴他。小明想著趕一場電影，那裏把阿林的「演講」聽進去。他只約略聽到一條曲線下的面積可以用畫格子的方法來算，那就是微積分。所以當他看到稻田一塊一塊地排著，就像昨天阿林劃在紙上的一樣。他就衝口說出可以用微積分算的話來。他有點後悔，不該說溜咀。又後悔沒好好聽阿林的「演講」，否則今天就可以向小華炫耀一番。這時候的阿林彷彿佛光高照，滿臉微笑，瞧著小明：「怎樣！後悔了吧！」

經小明、小華的要求，阿林開口了，滔滔不絕，恨不得把一肚子的微積分全吐出來：

其實微積分是微分和積分的合稱。剛剛你們吵什麼身子左右幌動，前仰後合都是因為車子的速度有了變化的緣故。我們這個世界是動態的：地球環繞太陽而轉；地球上風的吹送。四季的輪換，潮汐的升降沒有不是動的；甚至一個人睡在床上，他的血液還在循環。就連微小的電子，基本粒子，它們都是不斷地以高速在運動著。位置的變化就是速度，速度的變化率就是加速度。研究這些變化率的就是微分。至於求面積的方法則是積分研究的對象。那麼為什麼要把微分和積分扯在一起呢?這得談點歷史了。

每個人都知道微積分是牛頓和萊布尼滋發明的。但積分的觀念卻源遠流長，可以追溯到西元前三世紀。通常微積分課本都是講微分然後再講積分；而事實上，微分也比積分來得容易。可是歷史的發展卻正好相反：人們先考慮積分的問題，然後才考慮到微分的問題。

西元前三世紀左右正是希臘數學鼎盛的時侯。前有尤多緒斯(Eudoxus)。接著有歐幾里得，然後由阿幾米得集其大成。他們用一套窮舉趨近法 (method of exhaustion) 算出了很多圖形的面積，幾何體的體積以及曲線的長度。譬如阿幾米得首先算出圓的面積和圓周的長度，也就是說圓周率的近似值。他還算出球體的體積和球面的面積，橢圓形的面積、圓柱、圓錐的面積和體積等等，他所用的方法就是傳統的窮舉趨近法。但事實上這種趨近法的極限值，是很難計算的，有人不禁要懷疑他是怎樣得到結果的。我們知道阿幾米得也是靜力學和流體力學的鼻祖，他很漂亮地把桿桿原理應用到某些圓形上，而計算出這些圓形的面積。

「桿槓原理和面積又可以扯上關係？」

當然囉，這就是阿幾米得偉大的地方。

從阿幾米得以後雖然也出過偉大數學家，但是很少有人繼承他的工作。一直到十七世紀初，他的求積觀念才再度被重視，被研究。

文藝復興以後，物理學方面有了迅速的發展。其中最值得一提的就是開卜勒 (Kepler) 的行星運行三定律和伽里略 (Galileo) 的落體運動。由於對於物理世界深入探討的結果，發覺為了研究這個動態的世界，我們往往須要探求某些數量的變化率。而在幾何方面，複雜曲線的研究往往從曲線的切線著手，而切線正代表曲線的變化率。這兩方面發展的結果逐漸成了微分學。

在牛頓、萊布尼滋以前．所有有關面橫和變化率的探討大概都是個案的，沒有統一簡便的方法。直到他們的手中，微分和積分才有了系統化和符號化的研究，同時他們更發現微分和積分大體說來是互為反運算的，就像乘法和除法一樣，相互間有密切的關係。這個發現使許多觀念得以澄清，許多計算得以簡化，而且使微分和積分的運用大為推廣。這就是為什麼我們把微分和積分合在一起而稱為微積分的緣故。

「這麼說來，微積分並不是在他們手中無中生有的了！」

當然，任何發展、任何發明都不是無中生有的。牛頓說過：我不過是站在前人的肩頭上而已。這句話是相當有道理的。

好了，說了這麼多。我們先去玩玩，回去後再把微積分慢慢告訴你們。

第二天，小明和小華按捺不住好奇心，相約一起去找阿林。

小華搶著說道：「怎麼用積分來算稻田有多少塊呢？」

阿林拿著筆在白紙上劃了一條直線說道：「這就代表那條公路。」按著又劃了一條曲線代表山腳邊，然後把田地也都劃出來了。

「標有1號的田地是整塊的．而標上2號的田地都不是整塊的，所以照這個圖來看，稻田的個數應該在21塊到28塊之間。嘿！小明有什麼問題？」（如圖二）

圖二

「這就是微積分了？這樣算面積誰都會的。」

「不錯，一塊一塊算出它的面積就是求積分。積分不來並不是什麼深奧的東西，至於微分，那是求一個函數的變化率，這部份以後再談，我們現在先談談積分。」

「那麼我們要微積分──不，積分幹嘛？」

「積分就是用來求面積。你已經在求面積了，怎麼說積分沒用呢？」

「不是！」小明急辯道：「我是聽說積分有很多學問，是很難的東西。但照你這末說，好像只是簡單算算它有幾塊田地而已。這是連小學生都會的呀！」

「對啦！這才是你要問的問題，是不是？」阿林慢條斯理地：「其實你剛才問的也不錯，積分還有很多其他用途，不光是算面積而已，這點待會再講。先回答你目前的困惑。就從你最初的話談起。你說，到底田地面積是多少？」

「不是二十一塊到二十八塊嗎？」

「是的，但這不夠精確。我問的是「到底」有幾塊？」

「……」

「這就是你認為積分『很有學問』的地方了。通常我們能算的面積都是正方形、長方形或多邊形等等。這些圖形的周界都是由直線的一部份圍成的。但如有一邊不是直線。而是曲線，問題便不簡單了。你說該怎麼算？」

「是呀！該怎麼算？」

「這就是積分的問題了。就是我們要分田地的緣故了，那些不靠曲線的都是小方塊，而方形的面積是可以算的……。」

「但你剛才不是說，這不夠精確嗎？」小明忍不住插口。

「對的，但我們可設法弄得更精確些。我們可以把一塊田的每一邊分成兩等分而得到四片田地。這樣剛才一些靠邊不是整塊的都份，又有一部分屬於小方塊。於是這次小方瑰的總面積就更靠近實際面積。如此這般，當我們把田地分得越細小，所算出的面積就越精確。求面積的整個觀念就是這麼簡單。（如圖三）

圖三

小明想了一想說：「那麼我們有沒有辦法算出真正的面積來呢？」

阿林皺了皺眉頭：「這個問題可大了。首先我們必須弄清楚什麼叫做一塊土地的真正面積。譬如一個以一公尺半徑的圓形土地，它的面積是圓周率乘上半徑的平方，也就是π平方公尺。那麼π用實際數字表示出來是多少呢？」

「3.1416」小華搶著說。

「你呢?」阿林望著小明。

小明想了一下，說：「我只能說3.14159...... 但點點是什麼我就不知道了。」

阿林笑了笑說：「怎麼樣？問題不簡單吧，就是最常見的圓面積也不能用一個較簡單的整數，有限小數或循環小數表示出來。這三類較熟悉的數叫有理數，而圓周率卻屬於『無理數』，是個不循環的無限小數。我們雖然理論上可以算出任何位的正確小數來。」

「那麼，圓周率到底是怎麼求得的呢？而圓的面積又該如何計算呢？」

「圓周率的求法有很多種。現在我們既然在談面積，我們就用窮舉趨近法來求圓的面積。如果這個圓的半徑是一公尺，我們求出圓面積便等於求出圓周率了。」

「是不是用像剛才畫格子的辦法？」

「你可以用那種方法。但因為圓是個太規則的圖形，我們可用更巧妙的辦法──我們可用正多邊形的方法來趨近它。

圖四

假定我們做了圓內接正四邊形和外切正四邊形顯然地，圓面積一定介在這兩個正方形之間。外切正四邊形每邊長2，所以面積（叫它作 P₁）是：

P₁= 2² = 4

內接正四邊形每邊長為 $\sqrt{2}$ ，所以它的面積是

$\begin{displaymath}q_1=(\sqrt{2})^2=2 \end{displaymath}$

於是圓面積（叫它作S）一定大於2而小於4，即 q₁<s<p₁

圖五

但這樣太不準確了。如果我們把四個圓弧中點作切線或弦，我們係得內接與外切正八邊形：你看，內接正八邊形的面積一定大於內接四邊形的。而外切八邊形的卻小於四邊形。事實上，我們可算出外切八邊形面積 P₂

$\begin{displaymath}{\bf P}_2=8(\sqrt{2}-1)\cong 3.312......\end{displaymath}$

及內接正八邊形面積 q₂：

$\begin{displaymath}q_2=2\sqrt{2}\cong 2.828......\end{displaymath}$

照這樣算下去，我們繼續求十六邊形，三十二邊形等之，但無論如何，圓面積一定大於內接多邊形而小於外切多邊形。於是我們有：

$\begin{displaymath}q_1 < q_2 < \cdots \cdots <q_n< \cdots \cdots < S < P_n < \cdots \cdots < P_1 \end{displaymath}$

這樣，對應於每個正整數 n，就有個實數 q_n，我們就說

$\begin{displaymath}\{q_1,q_2, \cdots \cdots q_n\}=\{q_n \}\end{displaymath}$

是一個數列。同樣，{p_n}也是個數列。n愈大，p_n 與q_n愈接近，常然更接近夾在當中的真正圓面積。我們就說q_n與p_n趨近S,或用數學式子寫這句話：

$\begin{displaymath} \lim_{n \rightarrow \infty}{\bf P}_n=\lim_{n \rightarrow \infty}q_n =S(=\pi) \end{displaymath}$

而說這兩個數列是收歛的(Convergent)，其收斂值為 S。用這種窮舉趨近法，我們便可得到一個數值，這便是我們所要的「真正面積」。

反過來，如果我們先只有兩數列 {p_n} 及 {q_n} 滿足

$\begin{displaymath} q_1<q_2< \cdots \cdots <q_n< \cdots \cdots < P_n< \cdots \cdots < P_2<{\bf P}_1 \end{displaymath}$

同時q_n和p_n可以任意接近，我們就說數列{p_n}及 {q_n}決定了一個實數。在上面這個例子中．被決定的實數就是圓周率π。

因此我們要了解積分，必先了解實數。部份的實數（有理數）是較熟悉，但另部份則不常見。事實上，實數觀念是純抽象的。經過了幾千年的努力，人類才能對實數作有系統的研究，從正整數到分數到零和負數，最後到實數，每一觀念的形成都要經過幾百年甚至幾千年之久。直到十九世紀下半葉才有數學家對實數做了嚴格的定義。其中的一種定義就是前面所說的兩數列決定一實數的方法。

我們從「真正面積」談到數列，數列的收斂以及實數，這似乎扯得太遠。但是為了懂得什麼是真正的面積以及怎樣計算它，這些觀念是不可少的。

「可是每次這麼算，不是太複雜麼？」

「不錯，這正是積分觀念由來已久而其應用最近才普遍的緣故。這是因為直到牛頓與萊布尼滋發現積分是微分的反運算後，才有較簡潔的算法。」

「別扯太遠了，還是來談面積吧！」

阿林想了想，說：「好吧，現在我們就來看看阿幾米得考慮過的一個算面積的例子。從這個例子，我們也可看出『真正面積』應該是什麼。」

阿林畫了一個圖：f(x) = X²

「這個函數畫出來的圖形，叫做拋物線。我們要的是算曲線下斜線部份的面積。」

「拋物線？」小明連想到丟石子的軌跡：「這個面積是什麼意思？」

圖六

「哦！我該先提一些積分的應用以及通常求積分的方式。積分是求面積，但我們可把這個『面積』的意義擴大。好比班上有五十位同學、在一次抽考中，50分到60分5人，60分到70分有20人，70分到80分有15人，80分到90分10人，我們可畫成如下圖形：

圖七

那麼樓梯形「曲線」底下的面積便可用來表示人數。譬如我們要知道有多少人及格，只需算在60分右邊的總面積便成。

在這裏，分數是以100分為一級，人數也不夠多，所以曲線是一條折線，如果在大專聯考，人數上萬，分數又算到小數點兩位數，畫出來的曲線便很平滑，可能像：

圖八

於是如果我們要知道30分到40分有多少人，我們只消求斜線部份的面積便成了。

類似這樣的例子很多，如果把分數（即橫軸）改為年代，把人數（即縱軸）改為當年的出生人口，那麼斜線的面積便代表某年到某年出生人口的總數。又如橫軸代表時間，縱軸代表一個商店當時出售貨物的數量，面積便是代表某段時間內總共賣了多少東西。橫軸代表離家距離，縱軸式代表你走到那兒淋雨的多少，面積便代表落湯雞的程度等等。」

「哦！難怪積分有這麼大的用途。」

「當然，從物理、化學到生物，乃至於商業、經濟、社會等等，都會用到。只要我們研究的對象，有些性質（可用數量表示出來）會因時間、位置或其他因素而變化，我們就說得到一個函數。函數告訴我們，任某一時間（或地點或其他因素）該性質的數值。積分後便是某段什間（或距離等）的總數值。

科學的研究便是經常將對象的性質拆成一小片一小片各求其值。要知道整體的效果，只要把它全部加起來，這就是積分。

我們又扯太遠了。還是回到阿基米得的例子。現在我們可知道一條拋物線也許代表某種數量因時間或地點而變化的關係。因此求面積便是求某個總數量。讓我們就來算斜線部份的面積。」

阿林再拿起筆來，重新畫一個圖：

圖九

「就像算田地的面積那樣，我們畫些格子……」

「但這次你畫的並不是正方格子。」

「那無所謂。畫格子的只是用來算面積。長方格子我們照樣可算它的面積，我們甚至可畫梯形，如下圖：

梯形（斜線部份） $= \frac{(f(b)+f(a))(b-a)}{2}$

圖十

或任何其他形狀；而且也不必平均分成幾份（可以有些格子寬、有些窄）。只要分出的形狀是可以計算出面積的，而且可以繼續細分，使格子總面積趨近曲線下面積便行。

但現因我們要求出一個易於計算的公式，我們就把 b 平均分成 n 等分。每一小段的長度便等於 b/n。那麼每個長方塊。譬如 MNQP 的面積是多少呢？」

「是 PM 乘 MN。」

「不錯。但 PM 多長？MN 多長？」「MN 長 b/n，但是 PM……。」

這就是我們要用 f(x)=x² 函數的理由了。因為我們可以用這個函數求出 PM 值。假定 M 是第 K 個分點，即 M 點座標 $\frac{k}{n}b$ （為什麼？）你很快便可算出 MP 長 $(\frac{k}{n})^2b^2$ ，而長方形面積就是：

$\begin{displaymath}\frac{b^3}{n^3}k^2\end{displaymath}$

把所有長方形面積加起來（就是讓 K 分別靠於 1,2, ... n-1），我們便可算出面積 P_n 等於：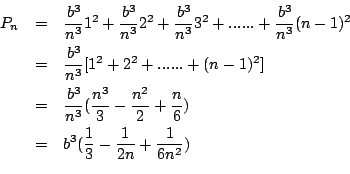

$\begin{eqnarray*} P_n&=&\frac{b^3}{n^3}1^2+\frac{b^3}{n^3}2^2+\frac{b^3}{n^3}3^2... ...rac{n}{6})\\ &=&b^3(\frac{1}{3}-\frac{1}{2n}+\frac{1}{6n^2})\\ \end{eqnarray*}$

「正如算圓面積時，同時用內接及外切多邊形一樣，在此我們也可用下列長方形分法：如下圖不同的是這次面積都比曲線面積大。你可以用同法算出所有矩形面積和為：

$\begin{displaymath} q_n=\frac{b^3}{n^3}(\frac{n^3}{3}+\frac{n^2}{2}+\frac{n}{6}) =b^3(\frac{1}{3}+\frac{1}{2n}+\frac{1}{6n^2}) \end{displaymath}$

顯然，我們有：

$\begin{displaymath} P_1 < P_2 \cdots < P_n \cdots < q_n < \cdots < q_3 < q_2 < q_1 \end{displaymath}$

而且

$\begin{displaymath} \vert q_n-P_n\vert=\frac{b^3}{n} \end{displaymath}$

當 n 很大時，p_n 和 q_n 便可任意接近。所以數列 {p_n} 和 {q_n} 便決定了一個實數，這個實數就是曲線下的『真正面積』。「這就要算 P_n 和 q_n 的收斂值了。當 n 很大時， $\frac{1}{2n}$ 和 $\frac{1}{6n^2}$ 就很小，可以小到比你說的固定正數都小，也就是無限靠近 0。於是在極限時，這兩項便可略去，用數學式子來寫：

$\begin{displaymath} \lim_{n \rightarrow \infty}P_n=\lim_{n \rightarrow \infty} \{b^3(\frac{1}{3}-\frac{1}{2n}+\frac{1}{6n^2}) \}=\frac{b^3}{3} \end{displaymath}$

同樣

$\begin{displaymath} \lim_{n \rightarrow \infty}q_n=\lim_{n \rightarrow \infty} \{b^3(\frac{1}{3}+\frac{1}{2n}+\frac{1}{6n^2}) \}=\frac{b^3}{3} \end{displaymath}$

兩者都是 $\frac{b^3}{3}$ ，於是曲線下的面積便是 $\frac{b^3}{3}$ 了，這就是阿基米得遠在積分和微分的關係被發現前便算出的公式。」

「它還是很麻煩嘛。」

「不錯。微積分發展後，我們就有較簡單的方法來計算。但麻煩也有點好處，我們可從過程中發現積分的真正意義。如果只會簡單方法，很可能你只學到公式化的計算，只會解書本上的習題。遇到許多實際的問題，需要你去理解、分析，你便可能不知所措。缺乏創意了。」

「好了，今天我們已談得很多了，關於那種較簡單的求積分法，我們得先了解微分的內容。而微分本身就是一門大學問，不是三言二語可以說完的。我們留待下次再談罷！」

圖十一

對外搜尋關鍵字：
．微積分
．微分
．積分
．牛頓
．萊布尼滋
．尤多緒斯
．歐幾里得
．阿幾米得
．窮舉趨近法
．圓周率
．開卜勒
．收歛
．實數
．微分方程式

　1│2│3　


	（若有指正、疑問……，可以在此留言或寫信給我們。）

EpisteMath (c) 2000 中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有

編輯：洪瑛 ∕ 校對：黃信元 ∕ 繪圖：簡立欣

最後修改日期：3/19/2002