| |
|
4.遞疊對數定理(Law of Iterated Logarithm): |
有第三節的開始我們提到了弱大數法則的缺點。其實強大數法則也有同樣的問題。
譬如說在例2.1中我仍只知道在賭博次數 n 相當大時,甲方所得 Sn 介於 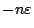 與
與 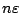 之間。由於 ε 可以任意小, 之間。由於 ε 可以任意小,
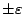 並不能視為對Sn
的一個很好的估計。LIL則確切地告訴我們 Sn 能好或壞到什麼程度: 並不能視為對Sn
的一個很好的估計。LIL則確切地告訴我們 Sn 能好或壞到什麼程度:
在與中央極限定理相同的假設下,
由對稱性,
此處和以下出現一對數函數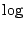 都是以e為底的自然對數。讓我們先解釋一個數列 都是以e為底的自然對數。讓我們先解釋一個數列
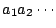 的 的 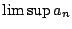 及 及 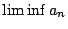 的意義。如果我仍把數列{an}
看成一個集合,且在實數軸上逐一點出,那麼有些點的附近會被一再地點到,這種點我們稱做數列{an}
的叢聚點(accumulation point)。數列{an}的叢聚點可能有很多個,其中最大的一個我仍就把它記成 的意義。如果我仍把數列{an}
看成一個集合,且在實數軸上逐一點出,那麼有些點的附近會被一再地點到,這種點我們稱做數列{an}
的叢聚點(accumulation point)。數列{an}的叢聚點可能有很多個,其中最大的一個我仍就把它記成
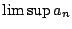 ,至於 ,至於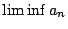 則是指叢聚點中最小的一個。譬如 則是指叢聚點中最小的一個。譬如
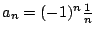 ,則 ,則
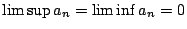 ,這時 ,這時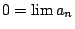 ,
所以 ,
所以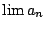 與{an}的最大點 與{an}的最大點
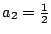 並不一樣。又譬如 並不一樣。又譬如
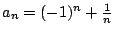 則
則
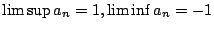 ,此時因兩者不相等, ,此時因兩者不相等,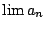 不存在。 不存在。
根據LIL,在例2.1中甲方賭博n次所得Sn滿足
而且有許許多多次。(即有無窮多個n),
這個結果比強大數法則的
要準確多了,注意此處的 n 可能隨著賭局而變動,也就是說 n 是 w 的函數。
同樣的道理在(2.3)式中的Sn滿足
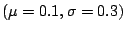
換句話說我們不但知道數位0在x的小數展開裡出現的頻率是0.2我們也知道幾乎所有的x
的小數展開式前面n個位數中0出現約達
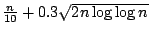 次的這種n有無窮多個。 次的這種n有無窮多個。
|
|
|