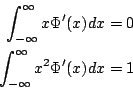| |
|
3.中央極限定理(Central Limit Theorem): |
弱大數法則有些地方不盡完善,因為對任意事先選定的正數ε,不論它是多小,
這表示用 n 來除 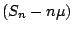 是稍微大了些。那麼是否可以找到一個比 n 小的尺度,用它來除 是稍微大了些。那麼是否可以找到一個比 n 小的尺度,用它來除 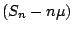 時我們可以得到一些有意思的結果呢?中央極限定理是這個方向的重要結果。 時我們可以得到一些有意思的結果呢?中央極限定理是這個方向的重要結果。
- 中央極限定理:
設 X1,X2,… 是 i.i.d.,且
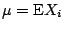 及變異數 及變異數
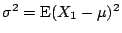 皆存在,則對任意實數 x,
皆存在,則對任意實數 x,
上式的 Φ 就是有名的標準正規分佈函數 (Standard normal distribution),或稱 Gauss分佈函數,因為 Gauss 在研究天文測量的誤差問題時發現了它
編者註
。Φ 的期望值 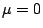 ,變異數 ,變異數 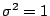 : :
由於 Φ 在統計上的重要性,Φ 的數值有表可查。譬如
- 例3.1
雖然(3.1)式是一極限,在實際計算 Fn(x) 時,我們常用
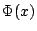 來取代 來取代
或者
許多時候這種取代所導致的誤差相當小。設例2.2的 Bernoulli trial 的
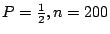 ,
我們想要計算 ,
我們想要計算
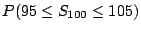 即在200次投擲一公正銅板當中,
正面出現的次數介於95到105次的概率。顯然地, 即在200次投擲一公正銅板當中,
正面出現的次數介於95到105次的概率。顯然地,
但右式並不容易計算。利用(3.3)式,因
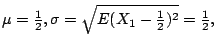
與正確值 0.56325… 的誤差不到 0.02%。
讓我們再看另一個情形。當 p=0.1,n=500,
與正確值 0.3176… 的誤差約 2%。
- 注意:
第一個情形誤差較小的理由是
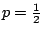 ,故 Sn 的分佈是對稱的。 ,故 Sn 的分佈是對稱的。
- 例3.2 保險問題:
假如某甲(或某機構)只有一棟房子,那麼毫無疑問地每個人都會建議某甲投保火險,
以確保他的財產安全。如果某甲有1000棟房子,那麼某甲是否仍該為這1000棟房子全部投保呢?
讓我們假設房子是分散各處。因此,某一棟房子遭受火災與否與其他房子無關。令
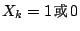 表示第k棟房子在今年遭受或未遭受火災,於是
表示第k棟房子在今年遭受或未遭受火災,於是
就住表今年某甲房子遭到火災的總數,
根據歷年來的統計資料我們可以估計每一棟房子在一年內遭到火災的機率,
為方便計我們假設每棟房子遭火災的機率都是 p
P(Xk=1)=p
P(Xk=0)=1-p
於是 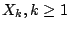 ,i.i.d.的 Bernoulli trial,根據中央極限定理我們可以估計S1000 的分佈情況。 ,i.i.d.的 Bernoulli trial,根據中央極限定理我們可以估計S1000 的分佈情況。
以上說法也適用於保險公司。唯一的差別是向它投保火險的房子總數更大,也因此(3.3)更加適用。現在讓我們來看看保險費是如何計算的。大致上,保險費是保險公司利用 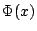 估算它每年將賠償客戶的總數及保險公司所賺利潤的總和。 估算它每年將賠償客戶的總數及保險公司所賺利潤的總和。
由於在一般情況中央極限定理已能應用於 S1000,我們似乎可以建議某甲不投保火險,從而省下將被保險公司賺去的利潤。從這裡我們也可了解為何當某甲只有一棟房子時他該投保。蓋此時數目太小,中央極限定理無法派上用場。
- 例3.3 假設檢定(Testing Hypothesis):
在科學上我們經常會做一些假設 (hypothesis) 來解釋一些現象。由此可知用實驗數據 (data) 來檢定,假設正確與否是一件重要的事。
假設某人在900次投擲一銅板中記錄到496次正面,究竟某人可否視此銅板公正?
假設是公正,應用中央極限定理於例2.2的
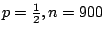 的情形 的情形
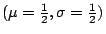 。 。
換句話說在1000次的類似情形裡,正面出現次數高過496的次數約只有2次。因此,
我們大致可認為此銅板不公正。
- 例3.4 座位問題:
假設甲、乙公司每天都各自有一輛設備完全相同的火車同時離開台北前往高雄,
假設n位旅客各自任意地選搭甲車或乙車,因此搭乘每一輛火車的人數是
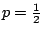 的n
次Bernoulli trial的結果。現假設甲車(或乙車)只有S<n個座位,因超S
位旅客搭乘甲車或乙車的機率f(s)是正數。此時就有旅客無位可座。根據(3.3)式 的n
次Bernoulli trial的結果。現假設甲車(或乙車)只有S<n個座位,因超S
位旅客搭乘甲車或乙車的機率f(s)是正數。此時就有旅客無位可座。根據(3.3)式
如果 s 相當大而使得 f(s)<0.01,那麼100次中的99次座位都會夠,更一般情況,公司可以事先決定一個失誤率α然後算出 s 使得 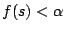 。譬如說,由(3.2)當 。譬如說,由(3.2)當
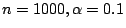 則 S=537 即足夠。如果兩家公司採同樣的失誤率0.01,則兩車共有1074個座位,其中74個將是空位,此種因競爭而導致的損失實在很小。同樣的道理,
每車若有549個座位就是足以應付1000次中的999次。 則 S=537 即足夠。如果兩家公司採同樣的失誤率0.01,則兩車共有1074個座位,其中74個將是空位,此種因競爭而導致的損失實在很小。同樣的道理,
每車若有549個座位就是足以應付1000次中的999次。
|
|
|