上頁　1│2│3│4│5│6　次頁

淺談機率上的幾個極限定理 （第 2 頁）

洋洋

 

首頁 | 搜尋

．原載於數學傳播九卷三期

•註釋
•對外搜尋關鍵字
 
1.基本概念

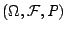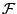機率空間 具有三個要素： $(\Omega,\mathcal{F},\textit{P})$，其中 Ω 是一個集合； $\mathcal{F}$ 是一些事件的集合，它是一個非空的 σ 域，具有下列性質：

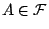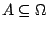
F1. 對每一 $A\in\mathcal{F}$， $A\subseteq\Omega$
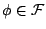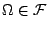
F2. $\phi\in\mathcal{F}$， $\Omega\in\mathcal{F}$
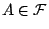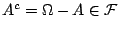
F3. 若 $A\in\mathcal{F}$ 則 $A^c=\Omega-A\in\mathcal{F}$
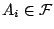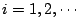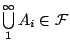
F4. 若 $A_i\in\mathcal{F}$，$i=1,2,\cdots$, 則 $\bigcup\limits^\infty _1A_i \in\mathcal{F}$

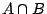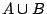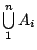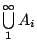所以若 A，B 是兩事件，則 $A\cap B$，$A\cup B$ 亦是事件。條件4或許不容易被立刻接受，高中課本上所討論的機率理論多半限於離散空間，在那裡我們只會遇到 $\bigcup\limits^n_1A_i$， 而不會遇到需無窮次運算的 $\bigcup\limits^\infty_1A_i$。

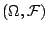機率空間的最後一要素 P 是 Probability 的簡寫，他是定義在 $(\Omega,\mathcal{F})$ 上的一個非負函數，具有下列性質：

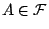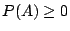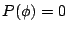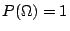P1.對每一 $A\in\mathcal{F}$，$P(A)\geq0$，且$P(\phi)=0$，$P(\Omega)=1$。
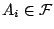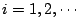P2.若 $A_i\in\mathcal{F}$，$i=1,2,\cdots$，彼此不相交，則

\begin{displaymath}P(\bigcup\limits^\infty_1A_i)=\sum\limits^\infty_1P(A_i)\end{displaymath}

由是我們可以推出

\begin{eqnarray*} P(A^c) &=& 1-P(A) \\ P(A\cup B) &=& P(A)+P(B)-P(A\cap B) \end{eqnarray*}


等公式。 用白話來說 P(A) 就是事件 A 發生的機率，所以若 P(A)=1 我們可以說事件 A 一定發生(嚴格來說應是 almost surely 發生)。譬如說，若 X 代表投擲一公平骰子時的點數，則

\begin{displaymath}P(X=1)=\frac{1}{6}\end{displaymath}

這表示投擲的結果是 1,2,3,4,5 或 6 的機會均等，換句話說， 平均起來在6次投擲骰子中有一次會出現1點，或者600次投擲中就恰有100次出現一點。請參見第二節的大數法則。

在正式介紹大數法則的等定理之前，我們還需要一些專門術語。

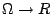我們稱X是Ω上的一個隨機變數 (random variable) 就是說 X 是 $\Omega\rightarrow R$ 的一個好函數(一般來說 X 的函數值不需要是實數)。所謂「好」係指在理論上我們能計算與X相關的一些機率，譬如

\begin{displaymath}P\{w:X(w)\in[a,b]\},a,b\in R\eqno{(1.1)}\end{displaymath}

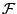用術語來說 X 是 $\mathcal{F}$ 可測，即對任意實數 $a,b\{w:X(w)\in[a,b]\}\in\mathcal{F}$。特別來說

\begin{displaymath}F(a)=P\{w:X(w)\leq a\}\eqno{(1.2)}\end{displaymath}

稱為 X 的分佈函數 (distribution function)。注意知道(1.1)與知道(1.2)是同一回事。

隨機變數X的期望值常用 μ 表示。依定義

\begin{displaymath}\mu=\mbox{E}X=\int^\infty_{-\infty}xdF(x)\end{displaymath}

當 X 的值域只有可數多點 a1,a2,…, 上式可化簡成

\begin{displaymath}\mu=\mbox{E}X=\sum\limits^\infty_{i=1}a_iP\{w:X(w)=a_i\}\end{displaymath}

譬如說 X 代表投擲一公正骰子所得的點數時，

\begin{displaymath}\mu=\frac{1}{6}(1+2+3+4+5+6)=3.5\end{displaymath}

我們稱隨機變數 X1,X2,…,Xn 是彼此獨立(mutually independent) 如果對任意 R 上的區間 A1,A2,…,An,

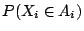\begin{displaymath} P(X_1\in A_i,X_2\in A_2,\cdots,X_n\in A_n) = \prod\limits^n_1P(X_i\in A_i) \end{displaymath}

注意上式中 $P(X_i\in A_i)$ 是

\begin{displaymath}P\{w:X_i(w)\in A_i\}\end{displaymath}

的簡寫。以後我們會經常採用此種簡寫。

我們稱隨機變數 X1,X2,…,Xn 是 i.i.d (independent and indentically distrbuted) 如果 X1,X2,…,Xn 除了彼此獨立外還有相同的分佈函數。統計上通稱 X1,X2,…,Xn 是依照 F 的隨機取樣 (random sample)，其中 F 是 Xi 們的共同分佈函數。

   

上頁　1│2│3│4│5│6　次頁

 回頁首
 
（若有指正、疑問……，可以在此 留言 或 寫信 給我們。）
EpisteMath

EpisteMath (c) 2000 中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有


編輯：趙竑鈞 ／ 校對：黃怡碧 最後修改日期：4/26/2002