古希臘幾何三大問題 (第 5 頁)

　1│2│3│4│5　

古希臘幾何三大問題（第 5 頁）

康明昌

首頁 | 搜尋

．原載於數學傳播第八卷第二期、第八卷第三期分兩期刊出
．作者當時任教於台大數學系

‧註釋
‧對外搜尋關鍵字

5.幾何三大問題不是幾何學研究的主流

方圓問題、三等分角問題與倍立方問題，雖然號稱幾何三大問題，可是在十八、十九世紀，並沒有太多的幾何學家研究這些問題。時代變了，幾何三大問題在古希臘的確是熱門的問題，在十九世紀卻逐漸失去其光彩。

十九世紀最熱門的幾何學是射影幾何 (projective geometry)。在 Carl Friedrich Gauss（1777～1851年）研究三度空間的曲面，Bernhard Riemann（1826～1866年）研究任意維數的微分流型之後，微分幾何 (differential geometry) 後來居上發展為一支數學主流。另一方面，Alfred Clebsch（1833～1872年）、Max Noether（1844～1921年）、Alexander von Brill（1842～1935年）嘗試把 Riemann 的 Abel 積分的理論建立在一個嚴格的幾何的基礎，終於建立了代數幾何 (alebraic geometry)，代數幾何也是現代數學的一支主流。從現在的觀點來看，十九世紀的幾何學家在留給後代的精神遺產中，以微分幾何與代數幾何最為珍貴。

在本節我們要簡略介紹十九世紀幾何學家的主要活動：非歐幾何、射影幾何、微分幾何 Erlangen 綱領與幾何學的基礎。我們不希望讀者以為幾何三大問題是幾何學研究的主要課題──完全不是這麼回事。

十七、十八世紀是微積分與分析學一支獨秀的時代。在解析幾何發展之後，傳統的幾何學家在氣勢上顯然輸人一截。從十八世紀末期法國大革命的時代，幾何學的研究又逐漸活躍起來。主要的原因是 Gaspard Monge （1746～1818年）把微分的方法引入幾何學的研究，利用幾何學的直觀來輔助微分方程的研究。Monge 又是一個第一流的教師，在他的帶領之下，Charles Dupin（1784～1873年），Victor Poncelet（1788～1867年）等一批幾何學家終於成長起來。根據 Flelix Klein 的講法，Monge 的書讀起來就像小說一樣，清楚流暢，不枝不蔓，到處是豐富活潑的想像力，隨時在顯示一個真正的幾何學家的標記：對形相的熱愛。

在介紹十九世紀幾何學家的主要活動時，我們想添敘一件事。十九世紀是幾何恢復活力的時代，有不少幾何學家很熱心的研究歐氏平面幾何的問題。例如，C.J. Brianchon（1785～1864年）與 Poncelet 證明九點圓定理：平面三角形三邊的中點、三個高的垂足、三個高的中點，這九個點共圓。Karl Wilhelm Feuerbach（1800～1834年）甚至證明九點圓的圓心位於 Euler 線上（內切圓圓心、外接圓圓心、重心，這三點共線，叫做 Euler 線），並且九點圓與該三角形的三個外切圓相切。這類平面三角形與圓形的古古怪怪的定理在十九世紀初期簡直如雨後春筍般的到處滋生。可是我們今天幾乎都不知道這些定理，在課堂上也不會教這些定理。這些三角形與圓形的美妙定理並沒有使我們對幾何的概念更加深刻，也無助於我們發展一種活潑清晰的直觀想像力 (intuition)，它像一些深奧的謎語滿足人類的好奇心。在解析幾何的威力籠罩下，這種謎語其實不猜也罷。

因此儘管這類的活動在十九世紀初期相當多，我們並不將其列為十九世紀幾何學家的主要活動；事實上，Felix Klein 的《十九世紀數學史》根本就不討論這些事。歷史的洪流會讓金子漂浮起來，也會把泥沙掩埋在河床底下。 ⁶

5.1 非歐幾何

Euclid （歐基里德）的《幾何原本》的第五公設說：「兩直線相交於內角和小於二直角的一側」。」這個公設就是大家熟知的平行公設。

很久以來，數學家就對這個公設不太舒服。相信連 Euclid 本人也不滿意，否則他不會把這個公設擺在最後面，直到非用不可時才提出來；並且他也不會把這個公設講得這麼彆扭。有些人想找一個看來比較順眼的公設代替它，有些人想從其他幾個公設導出這個公設。最有名的是把第五公設換成以下的平行公設：「過線外一點可作唯一的直線平行這已知線」。直到十八世紀後期，才有一些數學家逐漸相信平行公設是獨立於 Euclid 的其他公設。

真正的突破來自一份不太有名的俄國期刊。1829年 Nikolai lvanovich Lobatchevsky（1793～1856年）提出非歐幾何的概念，在這種幾何學裏，過線外一點存在不只一條直線平行於這已知線。 1832年 János Bolyai（1802～1860年），奧匈帝國的一個軍官，也獨立的提出相似的結果。事實上早在 Lobatchevsky 與 Bolyai 之前，偉大的 Gauss 早已開始研究非歐幾何學，只是沒有發表而已。

Lobatchevsky 的想法可以簡單的描述如下。他同意歐氏幾何的其他公設，只把平行公設改變。設 AB 是已知直線，C 是線外一點，a 是 C 點到 AB 的距離。Lobatchevsky 假設對於這樣的 C 點與 AB，必存在一個角度 $\pi(a)$ （隨 a 的大小而改變），使得通過 C 點的直線分成兩類：一類直線與 AB 相交，這些直線與 CD 的夾角小於 $\pi(a)$ ；剩下一類直線不與 AB 相交，這類直線最邊界的是直線 p 與 q，p 與 q 就是通過 C 點的「平行線」。Lobatchevsky 決定，

$\begin{displaymath} 0\leq\pi(a)\leq\frac{\pi}{2} \; \mbox{{\fontfamily{cwM0}\fon... ...es{m}\selectfont \char 47}} \; \pi(a)=2\tan^{-1}\frac{1}{e^a} \end{displaymath}$

因此，若 C 在 AB 上， $\pi(a)=\frac{\pi}{2}$ ，這兩條平行線與 AB 重合；若 C 在無窮遠處， $\pi(a)=0$ 。由此他能導出三角公式，

$\begin{eqnarray*} \cot\pi(a)&=&\cot\pi(c)\cdot\sin A\\ \sin A&=&\cos B\cdot\sin\pi(b)\\ \sin\pi(c)&=&\sin\pi(a)\cdot\sin\pi(b) \end{eqnarray*}$

令人驚奇的，這些三角公式竟和球面三角的公式極相像：只要我們把球面三角的 a,b,c 換成 ia,ib,ic，就得到非歐幾何的三角公式。

在這種幾何空間中，三角形的三內角和小於 π。半徑為 r 的圓的周長是 $\pi(e^r-e^{-r})$ ，面積是 $\pi(e^{\frac{r}{2}}-e^{-\frac{r}{2}})^2$ 。一般的說，如果 y=f(x) 是這種幾何空間上的曲線，其弧長元素是 $ds=\sqrt{(dy)^2+\frac{(dx)^2}{\sin^2\pi(x)}}$ 。

Lobatchevsky 幾何還可以用另一個觀點來瞭解，這是 Henri Poincaré（1854～1912年）提出來的。在 Poincaré 的模型中，我們考慮的「點」是圓內的所有的點（不含圓周上的點）；「直線」有兩種，一種是通過圓心的直線，另一種是與圓周正交的任意圓弧。兩點 P₁ 與 P₂ 的距離定為 $\ln(\frac{P_1P_b}{P_2P_b} \cdot \frac{P_2P_a}{P_1P_a})$ ，其中 P₁ P_a,… 是其歐氏幾何中的距離（如上圖）。

Lobatchevsky 與 Bolyai 提出非歐幾何的概念，最初並沒有引起數學家的注意。一般的人仍然相信歐氏幾何才是物理世界真正的幾何模型，非歐幾何只不過是邏輯正確的一套演繹體系而已。直到 Riemann 提出廣義的空間的概念，把 Lobatchevsky 與 Bolyai 的非歐幾何納入微分幾何的範圍之內，非歐幾何才被數學家心安理得的接納下來。Riemann 的微分幾何在 1916年被 Albert Einstein（1879～1955年）作為廣義相對論的基礎，人類才發現，歐氏幾何並不必然是物理世界唯一的幾何模型。

5.2 射影幾何

射影幾何是十九世紀幾何學家的主要戰場，歐氏幾何、非歐幾何、球面幾何的量度性質 (metric properties) 在射影幾何之內得到統一的處理，綜合學派（synthetic school, 以 Carnot、Poncelet、Steiner、Von Staudt、Chasles 為主）與解析學派（analytic school, 以 Möbius、Plücker、Cayley 為主）在射影幾何的研究展開白刃戰。利用射影幾何的觀點，許多古老的定理，如 Pappus 定理，Pascal 定理，被重新證明，許多新的方法和新的幾何概念被提出來。

射影的概念，是 Gerard Desargues（1593～1662年）最先提出的。有名的 Desargues 定理說：如果 $\triangle ABC$ 與 $\triangle A'B'C'$ 的對應頂點的連線 AA',BB',CC' 交於一點 O。令其對應邊 AB 與 A'B'，BC 與 B'C'，CA 與 C'A' 各交於 P,Q,R。則 P,Q,R 三點共線。(讀者不妨把 $\triangle ABC$ 與 $\triangle A'B'C'$ 想成落在不同的平面上，利用簡單的立體幾何，很容易證明 P,Q,R 共線。再考慮同一平面的情形。可是 Desargues 的射影幾何並沒有引起當時數學家的注意。

射影幾何的開創者應該算 V. Poncelet。Poncelet 是 Monge 在巴黎工藝學校的學生，1812年隨 Napoléon Bonaparte（拿破崙）遠征俄國，他在該年的冬季會戰被俘，囚禁在伏爾加河邊的薩拉托夫 (Saratov)。兩年的監獄生活使他創造了射影幾何。他在囚房中，對著一群同是工藝學校畢業的難友發表他的數學心得。在沒有任何參考書的惡劣環境下，他重新證明 Monge 與 Carnot 教過的定理，然後提出他自己新的結果。1815年回國之後，把這些結果發表，射影幾何於焉誕生。

Poncelet 提出射影 (projectivity) 的概念。例如，由 O 點把直線 l₁ 投射到直線 l₂，再由 O' 點把直線 l₂ 投射到 l₃。如是操作，幾次投射的結果就是射影。射影把 l₁ 的點一一對應到 l₃，例如 A 對應到 A''，B 對應到 B''。我們不只可以對直線作射影，我們也可以對平面作射影。

Poncelet 還提出對偶性 (duality) 的概念。在射影平面上，點和線互為對偶。因此 Desargues 定理的對偶定理變成：若有直線 l₁，l₂，l₃，與 l₁'，l₂'，l₃'，如果 l_i 與 l_j 的交點共線，i=1,2,3，令 l_i 與 l_j 交於點 P_ij，l_i' 與 l_j' 交於點 P_ij'。則直線 $\overline{P_{12}P_{12}'}$ , $\overline{P_{23}P_{23}'}$ , $\overline{P_{31}P_{31}'}$ 共點。（Desargues 定理的逆定理！讀者自己證明吧。）

此外 Poncelet 還提出連續性原理 (principle of continuity)、無窮遠線 (the line at infinity)、虛擬點 (imaginary points) 等等概念。

Poncelet 是一個不願意使用座標的綜合幾何學家。如果使用解析的方法，Poncelet 的許多概念都可以變成更加的明白清楚。

射影平面是歐氏平面再加上一條無窮遠的線。射影平面的每一點可以用座標 (x₀:x₁:x₂) 表示，其中 x₀,x₁,x₂ 不全為零。兩個座標 (x₀:x₁:x₂) 與 (y₀:y₁:y₂) 代表同一點，如果 $y_0=\lambda x_0$ , $y_1=\lambda x_1$ , $y_2=\lambda x_2$ ，λ是某一個不為零的數。歐氏平面可以看做 {(x₀: x₁:x₂):其中 $x_0\neq0\}$ 的點集合；如果把 $u=\frac{x_1}{x_0}$ , $v=\frac{x_2}{x_0}$ 代入，歐氏平面的點恰好和 {(1:w:v)} 的點一一對應。在歐氏平面上的直線方程式 au+bv+c=0，在射影平面變成 ax₁+bx₂+cx₀=0。歐氏平面的拋物線 v=au²，橢圓 $\frac{u^2}{a^2}+\frac{v^2}{b^2}=1$ ，雙曲線 $\frac{u^2}{a^2}-\frac{v^2}{b^2}=1$ 在射影平面分別變成 ax₁²-x₀x₂=0, a²b²x₀²-b²x₁²-a²x₂²=0, a²b²x₀²-b²x₁²+a²x₂²=0，似乎沒有太大的區別，無窮遠的線是 x₀=0。兩條直線必定相交。

射影平面的直線方程式既是 ax₀+bx₁+cx₂=0，我們不妨把直線的座標定為(a:b:c)。這樣說來，直線和點豈不是一一對應了？這就是 Poncelet 的對偶性。

如果在射影平面的點座標取自實數，就得實射影平面 (real projective plane)。如果容許複數出現在這些點的座標，就得到複射影平面 (complex projective plane)。 Poncelet 的所謂虛擬點只不過是複射影平面上的一個點。Poncelet 由實射影平面出發，卻不得不走到複射影平面。所謂的虛擬點並不虛無飄渺，而是理論的必然產物。

在複射影平面上，任何一個非退化的二次曲線，經過適當的座標變換，都可化成 x₀²+x₁²+x₂²=0 的形式（何故？請注意一個三階對稱矩陣必可對角化）。因此，在複射影平面，所謂拋物線、雙曲線、橢圓根本就是同一件東西。

Poncelet 的連續性原理可以用複射影平面的 Zariski topology 來解釋；我們姑且從略。

讀者如果想學習一點射影幾何，讓我推薦 R. Hartshorne,《Fundations of Projective Geometry》。

這本書從綜合幾何、解析幾何和運動群 (transformation groups) 三個觀點來探討射影幾何，是一本寫得相當精緻的小書。

把複射影平面加以推廣，就是 n 維的複射影空間 (n-dimensional complex projective space)，其中的點是 $(x_0:x_1:\cdots:x_n)$ ，x_i 是複數。所謂的代數多樣體 (algebraic variety) 就是在某一個 n 維複射影空間之內，滿足一組方程式的所有點的集合。例如，{ (x₀:x₁:x₂): x₀⁵+x₁⁵+x₂⁵=0 } 是複射影平面的代數多樣體。代數多樣體之上的幾何，代數多樣體的分類以及代數多樣體之上的函數論一直是從十九世紀以來代數幾何學家最感興趣的問題。

5.3 微分幾何

Monge 雖然把分析的方法引入幾何的研究，來討論曲線與曲面的各種性質，他並沒有把它們看作一個獨立存在的幾何對象 (geometrical object)。第一個把曲面看成獨立存在的幾何對象的是 Gauss（1827年）。

三度空間中的曲面的點 (x,y,z)，只要在足夠小的範圍，都可以用兩個參數 u， v 表示出來，即

$\begin{eqnarray*} x &=& x(u , v) \\ y &=& y(u , v) \\ z &=& z(u , v) \end{eqnarray*}$

寫成微分式，得

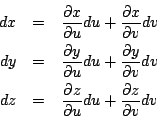
$\begin{eqnarray*} dx &=& \frac{\partial x}{\partial u}du+\frac{\partial x}{\part... ... \frac{\partial z}{\partial u}du+\frac{\partial z}{\partial v}dv \end{eqnarray*}$

因為弧長元素是 ds²=dx²+dy²+dz²，故

ds²=Edu²+2Fdudv+Gdv²

其中

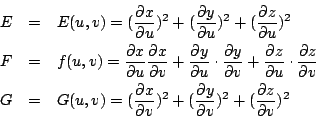
$\begin{eqnarray*} E&=&E(u , v) =(\frac{\partial x}{\partial u})^2+(\frac{\partia... ...rac{\partial y}{\partial v})^2+(\frac{\partial z}{\partial v})^2 \end{eqnarray*}$

例如 $\varphi:(a , b) \rightarrow \mathbf{R}^3$

$\begin{displaymath} t\vert\rightarrow(x(u(t) , v(t)) , y(u(t) , v(t)) , z(u(t) ,... ...)))\mbox{{\fontfamily{cwM0}\fontseries{m}\selectfont \char 1}} \end{displaymath}$

是曲面上的一條曲線，則從點 (x(u(t₀) , v(t₀)), y(u(t₀) , v(t₀)) , z(u(t₀) , v(t₀)) 到點 (x(u(t₁) , v(t₁)) , y(u(t₁) , v(t₁)), z(u(t₁) , v(t₁)) 的弧長是

$\begin{displaymath} \int_{t_0}^{t_1}\sqrt{E(u(t) , v(t))(\frac{du}{dt})^2+ 2F(u(... ...frac{du}{dt}\frac{dv}{dt}+G(u(t) , v(t))(\frac{dv}{dt})^2}\;dt \end{displaymath}$

Gauss 把 Edu²+2Fdudv+Gdv² 叫做曲面的第一基本式 (the first fundamental form)。第一基本式只由曲面本身決定，與其周圍的三度空間沒有關係。因此，只要知道第一基本式，就可以把曲面看做一個獨立的幾何對象來研究。Gauss 獨到的觀察是，曲面的許多重要的幾何性質只由第一基本式就可以確立了。例如曲率 (total curvature) 與測地線 (geodesics) 就是。

曲率是測度曲面彎曲的程度。直覺的反應似乎是這樣，如果不是在三度空間，怎麼看得出曲面在那裏彎曲，在那裏比較平坦？可是反過來說，想像有一隻只有二度感覺的小蟲，它什麼時候爬到山頂，什麼時候到達鞍部，什麼時候來到平地，難道自己一點也沒有感覺嗎？事實上，這是 Gauss 認為最重要的定理 (Gauss theorem egregium)：（高斯）曲率完全由第一基本式決定的。

測地線可以看作是歐氏平面的「直線」概念的推廣。例如，在球面的測地線就是大圓（過球的平面與球面的交集）。考慮大圓的優弧與劣弧，我們知道，通過球面兩點的大圓弧（即測地線）不一定是通過這兩點長度最短的曲線。

Gauss 除了考慮這種局部的幾何性質 (geometry in the small)，他也考慮大域性質 (geometry in the large)。例如，令 A 是曲面的三角形（三邊都是測地線），若其三內角是 α,β,γ，Gauss 發現

$\begin{displaymath} \int_AKdA=\alpha+\beta+\gamma-\pi \end{displaymath}$

因此，因為球面是曲率恒為一個正的常數，球面三角形的三內角和恒大於 π。因為 Poincaré 模型的非歐幾何的曲率恒為一個負的常數，三角形的三內角和恒小於 π。因為歐氏平面的曲率恒為零，因此三角形的三內角和恰好是 π。

1854年 Riemann 把 Gauss 的想法予以推廣。他把傳統的三度空間的概念擴大到任意維數的空間，弧長元素是這種空間最基本的幾何性質。具體的說，n 維空間之中點的一組座標如果是 (x₁,…,x_n)，令弧長元素

$\begin{displaymath} ds^2=\sum_{i , j=1 , \cdots , n}g_{ij}dx_idx_j \end{displaymath}$

其中

$\begin{displaymath} g_{ij}=g_{ji} , g_{ij}=g_{ij}(x_1 , \cdots , x_n) \end{displaymath}$

是 x₁,…,x_n 的無窮可微分函數。從這裏出發，Riemann 也可以考慮曲線弧長、曲率、測地線。

為了有效的研究這種 Riemann 幾何 (Riemannian geometry)，數學家必須把微積分作更進一步的發展。在微分方面，這就是 E.B. Christoffel, G. Ricci-Curbastr（數學家簡稱他為Ricci）與 Tulli Levi-Civita（1873～1941年）發展出來的張量分析 (tensor analysis)。在積分方面，有 Eli Cartan（1869～1951年）發展出來的微分式 (differential forms)。

用這些工具，可以在 Riemann 幾何上面考慮什麼叫做平行移動，那就是曲率張量 (curvature tensor) 的功用。也可以考慮不同點的切線空間 (tangent space) 之間的聯系 (connection, 或 Levi-Civita connection)。Levi-Civita 發現，並非只有弧長元素的幾何空間才有「聯系」的概念；他把「聯系」作為一個獨立的幾何概念來研究，因此得到了新的幾何空間，即 non-Riemannian geometry。

Riemann 的幾何觀點使人類對空間的認識得到前所未有的解放。一個由 n 個獨立的物理量所作用的物理體系，不正是一個 n 維空間嗎？因此，這種廣義的幾何概念正好擴大了幾何的應用。

讀者如果具有微積分的知識，可以參考以下的文章，

R. Penrose,〈The geometry of the universe〉, in 《Mathematics Today》, edited by L.A. Steen，與 S.S. Chern,〈General relativity and differential geometry〉, in《Einstein Centennial Symposium》, Inst. Adv. Study, Princeton, N.J. 1979. Addison-Wesley, 1980, Reading, Mass.

這兩篇文章很生動並且很深刻的介紹微分幾何的幾個基本概念，並且討論微分幾何與物理（尤其是相對論）的關係。

5.4 Klein 的 Erlangen 綱領

十九世紀出現了這麼多幾何空間，不免使數學家要重新想一想：什麼是幾何空間？如何把這些幾何空間分類？

Klein 的 Erlangen 綱領 (Erlangen program) 就是想用運動群的概念來把各種幾何進行分類。

以歐氏平面幾何而言，「二邊一夾角定理（SAS定理）」告訴我們，歐氏幾何容許的運動是保長運動 (isometry)。保長運動其實就是移動 (translation)、轉動 (rotation) 或它們的合成函數。如果把點的座標記為 (x,y)，則保長運動可以表示為

$\begin{displaymath} {x\choose y}\rightarrow{x\cos\theta+y\sin\theta+a\choose -x\sin\theta+y\cos\theta+b} \end{displaymath}$

考慮

$\begin{displaymath} G= \left\{ \begin{array}{cc} \pmatrix{ \cos\theta &\sin\thet... ...0&1 \cr } &: \theta , a , b \in \mathbf{R} \end{array}\right\} \end{displaymath}$

G 的任意元素都可以看成一種保長變換。在矩陣乘法下，G 變成一個群(group)。G 就是歐氏平面幾何的運動群。歐氏平面幾何所研究的長度、角度、中點、圓、橢圓、雙曲線、面積，在 G 的作用之下都維持不變。換句話說，長度、角度……這些幾何量都是運動群 G 的不變量 (invariant)。

Klein 在1872年就任 Erlangen 大學的教授。在同一年，他提出一個分類各種幾何的辦法，世稱 Erlangen 綱領。Klein 認為，所謂的幾何就是研究各種運動群的不變量；對於不同的運動群，就產生不同的幾何。

因此歐氏平面幾何對應的運動群是

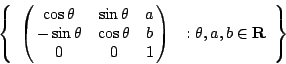
$\begin{displaymath} \left\{ \begin{array}{cc} \pmatrix{ \cos\theta &\sin\theta &... ...0&1 \cr } &: \theta , a , b \in \mathbf{R} \end{array}\right\} \end{displaymath}$

仿射幾何 (affine geometry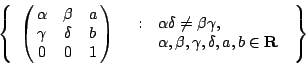) 的運動群是

$\begin{displaymath} \left\{ \begin{array}{cl} \pmatrix{ \alpha &\beta &a \cr \... ... \delta , a , b \in \mathbf{R} \end{array}\end{array}\right\} \end{displaymath}$

因此在仿射影幾何中，圓與橢圓也可以相互轉換。

射影幾何的運動群是

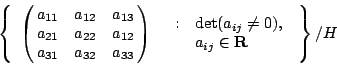
$\begin{displaymath} \left\{ \begin{array}{cl} \pmatrix{ a_{11} &a_{12}&a_{13} \... ...in \mathbf{R} \end{array}\end{array}\right\} \left/ H \right. \end{displaymath}$

其中 H 為

$\begin{displaymath} \left\{ \begin{array}{cc} \pmatrix{ \alpha &0 &0 \cr 0&\al... ... : \alpha \neq 0, \; \alpha \in \mathbf{R} \end{array}\right\} \end{displaymath}$

在射影幾何中，圓與雙曲線也可以相互轉換。射影幾何的不變量是「重合關係」(incidence relation)：如，一個點是否落在某條直線上（Desargue 定理、Pappus 定理所討論的就是這種幾何性質）。共線四點的調和比（harmonic ratio，或 cross ratio）也是射影幾何的不變量。

Erlangen 綱領當然不能把所有的幾何空間納入其體系。Klein 本人也非常瞭解這個事實，一般的 Riemann 空間通常都不能放在 Erlangen 綱領之內討論。不過 Erlangen 綱領畢竟提供一個新的研究幾何學的角度。

5.5 幾何學的基礎

自從非歐幾何出現之後，《幾何原本》已失去其唯我獨尊的地位。十九世紀末期，許多數學家發現《幾何原本》還有許多令人不能忍受的地方。例如，《幾何原本》說，直線是只有長度，沒有寬度的幾何對象，點只有位置，沒有長度也沒有寬度。用嚴格的數學標準來看，這些話究竟講了什麼呢？又如（見下圖），我們憑什麼能肯定的說直線 AP 與直線 BC 的交點一定落在線段 BC 之上？《幾何原本》的公理與定理似乎不能保證這件我們常用的事實。

Hilbert 的《幾何學的基礎》(Grundlagen der Geometrie) 重新整理平面幾何的公理（1899年）。Hilbert 把點、線、面的直觀聯想完全剝奪；他說，你也可以把點、線、面換個名稱，叫做椅子、桌子、啤酒桶。重要的是，各種定義與公理規定出來的點、線、面之間的相互關係，而不是點、線、面這些字面上的涵義。他非常小心的列出各種公理（包括幾個 Euclid 不自覺使用而沒有列出的公理），並且一再強調各種公理間的相容性 (consistency)、獨立性 (independent) 與完備性 (completeness)。經過 Hilbert 整理之後的平面幾何才變成邏輯上自足的演繹體系。

Hilbert 的工作固然徹底摧毀了《幾何原本》的崇高地位，但是它對幾何學的研究究竟有什麼重大的影響呢？我們已經看到，微分幾何和代數幾何安上局部座標 (local coordinate) 的裝備之後，早已奔上光明的前途，根本無瑕理會什麼公理體系是否完整自足。在有限幾何學 (finite geometry) 的研究可能還可以看到 Hilbert 的影響。個人認為，《幾何學的基礎》最大的作用是推動二十世紀某些數學部門（如，抽象代數、點集拓樸、泛函分析）的公理化過程，並且帶動數學邏輯的研究。

　1│2│3│4│5　


	（若有指正、疑問……，可以在此留言或寫信給我們。）

EpisteMath (c) 2000 中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有

編輯：黃信元

最後修改日期：5/3/2002