| |
- ...1
- 在放鬆這些條件時,例如,假設直尺可以刻劃,三等分角問題就可以進行了。有關這類變化,請參考 F. Klein,《Famous Problems of elementary geometry》。
- ...2
- 唸過抽象代數的人可能對我們在這裏的「體」的定義覺得不夠一般性。在抽象代數中,「體」是具有加法與乘法兩種運算的代數體系,這兩種運算具有某些特殊的性質。我們在這裏給的定義,其實是複數體之內的子體 (subfields) 的定體。歷史上來看,這種定義或下一個定義
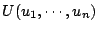 就是 Kronecker 所謂的「domains of rationality」,這是數學家最先瞭解的「體」。 就是 Kronecker 所謂的「domains of rationality」,這是數學家最先瞭解的「體」。
- ...3
- 要證明
![$\mathbf{Q}(\sqrt[3]{2})=$](img54.gif)
![$\mathbf{Q}+\mathbf{Q}\sqrt[4]{2}+\mathbf{Q}\sqrt{2}+\mathbf{Q}\sqrt[4]{8}$](img55.gif) 我們只要能夠把分母有理化即可。具體的說,對於任意的多項式
我們只要能夠把分母有理化即可。具體的說,對於任意的多項式
只要
![$g(\sqrt[4]{2})\neq 0$](img57.gif) ,我們都要有辦法把 ,我們都要有辦法把
![$\frac{1}{g(\sqrt[4]{2})}$](img58.gif) 變成 變成
![$a+b\sqrt[4]{2}+c\sqrt{2}+d\sqrt[4]{8}$](img59.gif) 的形式,其中 a,b,c,d 是有理數。因為 f(t)=t4-2 是 Q 上的不可約多項式,且 f(t) 與 g(t) 互質(否則 f(t) 是 g(t) 的因式, 的形式,其中 a,b,c,d 是有理數。因為 f(t)=t4-2 是 Q 上的不可約多項式,且 f(t) 與 g(t) 互質(否則 f(t) 是 g(t) 的因式,
![$f(\sqrt[4]{2})=0$](img60.gif) 故 故
![$g(\sqrt[4]{2})=0$](img61.gif) ),故可找到多項式 ),故可找到多項式 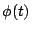 與 與 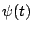 ,使 ,使
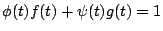 以 以 ![$t=\sqrt[4]{2}$](img65.gif) 代入,得 代入,得
利用
![$(\sqrt[4]{2})^4=2$](img67.gif) 的關係,可以把 的關係,可以把
![$\psi(\sqrt[4]{2})$](img68.gif) 化成 化成
的形式。
- ...4
- 令
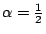 ,請讀者證明 ,請讀者證明
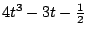 是Q 上的不可約多項式。 是Q 上的不可約多項式。
- ...5
- 若 α 與 β 是代數數,則
今 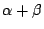 , , 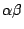
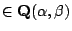 故 故
必定在 Q 上線性相依,其中 n 是某個正整數。因此 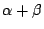 是代數數。或者,令 是代數數。或者,令
且 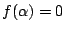 , ,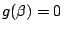 令 令
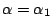 , ,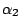 ,…, ,…,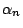 是 f(t)=0 的 n 個根,考慮 是 f(t)=0 的 n 個根,考慮
則
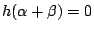 ,則 h(t) 的係數是 ,則 h(t) 的係數是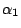 , ,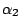 ,…, ,…,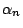 的對稱多項式,故 的對稱多項式,故
![$h(t)\in\mathbf{Q}[t]$](img114.gif) 。同理請讀者證明 。同理請讀者證明 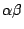 也是代數數。 也是代數數。
- ...6
- 有一段插曲。Klein 曾主持當時一套《數學百科全書》(Enzykiopädie der mathematische Wissensenschaften) 的編輯工作。他擬定許多主題,再邀請這些主題的專家寫作。其中一個主題就是要介紹類似 Feuerbach 定理這種初等幾何的結果。Klien 邀請 Max Simmon 寫這個主題。當 Simmon 寫好之後,Klein 改變主意了,他拒絕刊登這個主題。Klein 認為,像《數學百科全書》如此嚴謹的科學論著,是不容許這類初等幾何有任何立足的地方。因此,Simmon 只好自己出版他的論文,即 M. Simmon,〈Uber Entwicklung der Elementargeometrie in XIX Jahrhundert〉, 1906, Berlin.
|
|
|
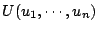 就是 Kronecker 所謂的「domains of rationality」,這是數學家最先瞭解的「體」。
就是 Kronecker 所謂的「domains of rationality」,這是數學家最先瞭解的「體」。
![$\mathbf{Q}(\sqrt[3]{2})=$](img54.gif)
![$\mathbf{Q}+\mathbf{Q}\sqrt[4]{2}+\mathbf{Q}\sqrt{2}+\mathbf{Q}\sqrt[4]{8}$](img55.gif) 我們只要能夠把分母有理化即可。具體的說,對於任意的多項式
我們只要能夠把分母有理化即可。具體的說,對於任意的多項式
![\begin{displaymath}g(t)\in\mathbf{Q}[t]\end{displaymath}](img56.gif)
![$g(\sqrt[4]{2})\neq 0$](img57.gif) ,我們都要有辦法把
,我們都要有辦法把
![$\frac{1}{g(\sqrt[4]{2})}$](img58.gif) 變成
變成
![$a+b\sqrt[4]{2}+c\sqrt{2}+d\sqrt[4]{8}$](img59.gif) 的形式,其中 a,b,c,d 是有理數。因為 f(t)=t4-2 是 Q 上的不可約多項式,且 f(t) 與 g(t) 互質(否則 f(t) 是 g(t) 的因式,
的形式,其中 a,b,c,d 是有理數。因為 f(t)=t4-2 是 Q 上的不可約多項式,且 f(t) 與 g(t) 互質(否則 f(t) 是 g(t) 的因式,
![$f(\sqrt[4]{2})=0$](img60.gif) 故
故
![$g(\sqrt[4]{2})=0$](img61.gif) ),故可找到多項式
),故可找到多項式 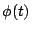 與
與 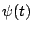 ,使
,使
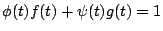 以
以 ![$t=\sqrt[4]{2}$](img65.gif) 代入,得
代入,得
![\begin{displaymath}\frac{1}{g(\sqrt[4]{2})}=\psi(\sqrt[4]{2})\end{displaymath}](img66.gif)
![$(\sqrt[4]{2})^4=2$](img67.gif) 的關係,可以把
的關係,可以把
![$\psi(\sqrt[4]{2})$](img68.gif) 化成
化成
![\begin{displaymath}a+b\sqrt[4]{2}+c\sqrt{2}+d\sqrt[4]{8}\end{displaymath}](img69.gif)
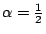 ,請讀者證明
,請讀者證明
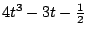 是Q 上的不可約多項式。
是Q 上的不可約多項式。
![\begin{displaymath}[\mathbf{Q}(\alpha , \beta):\mathbf{Q}]<\infty\end{displaymath}](img102.gif)
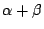 ,
, 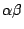
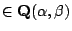 故
故
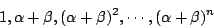
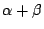 是代數數。或者,令
是代數數。或者,令
![\begin{displaymath}f(t) , g(t)\in\mathbf{Q}[t]\end{displaymath}](img107.gif)
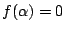 ,
,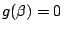 令
令
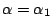 ,
,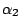 ,…,
,…,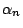 是 f(t)=0 的 n 個根,考慮
是 f(t)=0 的 n 個根,考慮
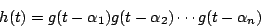
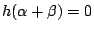 ,則 h(t) 的係數是
,則 h(t) 的係數是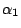 ,
,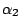 ,…,
,…,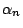 的對稱多項式,故
的對稱多項式,故
![$h(t)\in\mathbf{Q}[t]$](img114.gif) 。同理請讀者證明
。同理請讀者證明 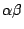 也是代數數。
也是代數數。