�ƪ����� �]�� 2 ���^
�d����
�D�����ƾǶǼ��Ĥ����ĥ|���B�ĤC���Ĥ@��
�D�@�̷��ɥ��Щ�x�j�ƾǨt
�E����
�E��~�j�M����r
|
�ƪ����� �]�� 2 ���^ �d����
|
�D�����ƾǶǼ��Ĥ����ĥ|���B�ĤC���Ĥ@�� �D�@�̷��ɥ��Щ�x�j�ƾǨt �E���� �E��~�j�M����r |
|
�Ҽ{�H�U�����D�P�u�ҩ��v�C
�H�W���u�ҩ��v��������~�O?
�ڭ̷Q�@�Q�A�H�W���u�ҩ��v���u�ҩ� n=1,2,3,4,5 �ɡA�즡���ߡC����
�b
����O�H�������O�H�H�������O����
���ǦP�ǥi��|���G�A�J�M���۫H�گ���ҩ� n=100�A�ڴN�ҩ����A�ݡC�A�u�n���ڤ@�p�ɪ��ɶ��A�ڴN�i�H�D�X 13, 23, 33, �K, 1003�A�A�D��M�A�M���ҩ��o�Ӧ��l�C
���D�N�b�o�ءG�A�n�Τ@�p�ɪ��ɶ��ҩ� n=100 �����ΡA�A�s���n�Φh�֮ɶ��~���ҩ� n=103 �����ΡH���~�A�b 103 ����A�٦��L�a�L�ɪ�����Ƶ��ۧA�@�Ӥ@�ӥh���ҩO�I
�M���Q�δX�N�l�]���O�q��@�y�s�h���A�]���@�y�s���d��O�������C�ڭ̲{�b���D���֤ߡA����ơA�O�L�����C�M�����s������k�A��M����ѨM�ڭ̪����D�C
�Q�ӷs����k�a�C
���]�ڭ̯���ҩ��u�Y k �O���N����ơA�åB n=k �ɭ즡���ߡA�h n=k+1 �ɭ즡�禨�ߡv�A����ڭ̴N�i�H���ө��|���ҩ��o���ڵ����F�C������O�H
�Ҧp�A�A�Q�ҩ� n=100 �ɭ즡���ߡA�̷ӤW�������]�A�A�u�n�ҩ� n=99 �ɭ즡���ߴN���F�C
���� n=99 �ɭ즡�|���|���ߩO�H�A�Τ@���ڭ̪����]�A�ڭ̥u�n�ҩ� n=98 �ɭ즡���ߴN���F�C
���� n=98 �ɭ즡�|���|���ߩO�H�A�Τ@���ڭ̪����]�A�ڭ̥u�n�ҩ� n=97 �ɭ즡���ߴN���F�C
�H�������A�ڭ̥u�n n=1 �ɭ즡���ߴN���F�C
��@�몺���A�ڭ̤��n�� n ���100�A�{�b�� n �O���N����ơC���w�ڭ̯���ҩ��ڭ̳̥������]�O���ߪ��A����u�n�ڭ̯���ҩ� n=1 �ɭ즡���ߡA�ڭ̴N�i�H���X n �O���N����Ʈɭ즡�禨�ߡC
�o�N�O�ƾ��k�Ǫk�C
�ƾ��k�Ǫk���n�I�O�G
�{�b�ڭ̧���D1.�����T���ҩ��g�b�U���C
�`�N:�@��ǥͦb�B�μƾ��k�Ǫk�ɡA�`�|�ǤU�p�U�����~�A�p
�u�ƾ��k�Ǫk�v�O�H���ܦ��N�D�`���x���u��C���b�j��þ�ɥN�AEuclid�]�ڰw�A��300B.C.�^�b�ҩ��u��ƬO�L�a�h���v�ɡA�w�g�x���F�u�ƾ��k�Ǫk�v���믫�]���U�@�p�`�����D1�^�C�H��\�h�ƾǮa������ı���Q�Ρu�ƾ��k�Ǫk�v�ҩ��U�ذ��D�C�Ĥ@�ө��T�����X�u�ƾ��k�Ǫk�v���Φ��P��z�A �O�k��ƾǮa Blaise Pascal�]�ڴ��� 1623-1662�^ 1 �C
|
|
���D2
|
�^�쥻�`����2.1�p�`�����D1�C�ڭ̭n�ҩ�13+23+�K+n3=
�P�ǥi��|��:�u�ڤ�����Q��o�ؤ�k�C�o�ؤ�k�n���O�q�ѤW���U�Ӫ��C���`���H�O�Q����o�ؤ�k���C�v ����N���ڭ̦A�Q�ӷs��k�a�C�P�����Ӥ��|�Ϲ�ϥΡu�k���Ҫk�v�a�C
���]�o�ӱԭz�O�����C�Ҧp�A�bn=199�ɡA13+23+�K+1993 �Ъ`�N�A �ڭ̲{�b�n�ɥX�@�ӥ٬ޡC
�]��
�� (1)-(2)�A ���O 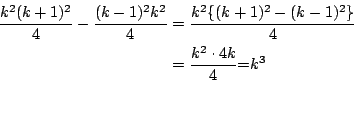
(3)����M�O�ӥ٬ޡC�ҩ������C
�H�W����k�i�H�`���p�U:
�ڦp�G���A�o�ءu�̤p�Ϩҡv����k�M��2.1�p�`�ҥΪ��u�ƾ��k�Ǫk�v���O�P�˪��믫�A�P�����ӷ|�P�N�F�a�C
�P�Ǥ����A�i�@�B�Q�Q�o�ءu�̤p�Ϩҡv����k�C�o�ؤ�k���O�Q�ΤF�۵M�Ƥ@�ӫ�����]���L�]�ܭ��n�^���ʽ�A�Y�G�۵M�ƪ����N�l���X�A�p�G�D�šA�@�w���@�ӳ̤p�������C
�o�өʽ���ܦ۵M�ƪ��j�p���Y�O�}�Ǫ��]well-ordered�^�C�@��ӻ��A�@�Ӷ��X�p�G�㦳�j�p���Y�A�Ҧp��ơB���z�Ʃι�ơA�o�ؤj�p���Y���O�}�Ǫ��A�p�G����@�ӫD�Ū��l���X�@�w�����@�ӳ̤p�������C��ơB���z�ơB��Ƴ����O�}�Ǫ��C�P�ǯण��b N x N �W���w�q�X�@�ب}�Ǫ��j�p���Y?�䤤 N �N���۵M�ƧΦ������X�C
���H�i��|�q���A�@�Ӷ��X�p�G�O�}�Ǫ��A�ڭ̤j���N�i�H�Q�Ρu�̤p�Ϩҡv����k�Ρu�ƾ��k�Ǫk�v�H���סG�������T�C�o�بҤl�b����������ƾDZ`�`�X�{�A���L�ڭ̤��dzƦb���~��l�s�U�h�C
|
�B�μƾ��k�Ǫk�ɡA�n�`�N�����ˬd:(1)n=1�ɬO�_���ߡA(2)�Yn=k�ɦ��ߡAn=k+1�O�_���ߡC�G�̯ʤ@���i�C�P�ɦb��(2)�B�J��k�A�O���N�@�Ӧ۵M�ơA�Ӥ��O�Y�ǯS�w���ơC
���O��
���b���ءH���b�S�����Ҳ�(2)�B�J�C
�bn=k�ɡA�o�ԭz���G�����W����k�I�Ҧb�@���u�W�A���p�o�O�諸�A�ڭ̷Q�ҩ������W����k+1���I�A�Ҧb�@���u�W�C
�] p1,�K,pk+1 ���o k+1 ���I�A�] p1,�K pk �� k ���I�A�G���̥��b�P�@���u�W�F�S�] p2,p3,�K,pk+1 �O k ���I�A�ҥH���̤]�b�P�@���u�W�C���O���N�G�I�K�M�w�@���u�A�ҥH p1,p2,�K,pk+1 �����b�P�@���u�W�A�]���Q���k�Ǫk�A�ڭ��ҩ��F�����W���N n �I�A�Ҧb�@���u�W�C
���O�G�ڭ̪�������T�I�A�K�i�ण�b�@���u�W�A����A�W�����u�ҩ��v���b���̡H
�bk=2�ɡA�ڭ̪��u�ҩ��v�o�Ͱ��D�C�bk=2���k=3�ɡAp1�Ap2�T�M�M�w�@���u�Ap2�Ap3�]�M�w�@���u�A�����̤��@�w���P�@���u�C�]��p1�Ap2�Ap3���@�w�b�@���u�W�I
�ڭ����ӧ��D�ا令�G�Y���N�T�I�Ҧb�@���u�W�A�h���Nn�I���b�@���u�W�C
|
|
���D3
|
�P�ǥi��|�ݡG�u�{�b�ڭ̤w�g�Ƿ|�ƾ��k�Ǫk�C�i�O�A�p�G���i�D�ڭ�13+23+�K+n3���M�O
�p��M�䵪�סH�����A�A�n������X�ӯS���Ҥl�F�b�o�ǯS�ҴM�䥦�̦@�P���B�A�ոլݯण���k�ǥX�@�몺���ץX�ӡC�P�ǥi�H�Ѧ� G. Polya�A�mHow to solve it?�n�o�O�@���ܭȱo�ݪ��ҥ~Ū���A���i�йت�����ҥ��A�����X�����X���C
�ڭ̦b�o�@�`�A�n���Ц��t�Ϊ��D�M��k�C
|
|
���D4
|
�P�ǭ̰����F�H�W���`�����D�P���D�A�|���|�u�k�ǡv�X�p�U���f�Z�G�u�ݨ�t��n���������Τ������ҩ��D�A�μƾ��k�Ǫk�v�H �p�G�A�o��g�H�ƾ��k�Ǫk�A����ЬݥH�U���Ҥl�C�A�μƾ��k�Ǫk�ҩ��A�ڥΧO����k�ҩ��A�ڭ̤��ɤ@�U�A���ݽְ����֡A�������C
[�Q�סG]
�L���g�H�ƾ��k�Ǫk���P�ǵL�צp�����ӥμƾ��k�Ǫk�ӸѸѳo���D�ءC�P�ǥi�H�Q�γo���D�ءA�ҩ�
|
|
|
|
|
�]�Y�������B�ðݡK�K�A�i�H�b�� �d�� �� �g�H ���ڭ̡C�^ |
|
|
|
EpisteMath (c) 2000 ������s�|�ƾǩҡB�x�j�ƾǨt �U�����峹���e���ۧ@�v����ۧ@�H�Ҧ� |
| �s��G����O | �̫�ק����G4/30/2002 |