- 1.回憶
為寫本稿，乃找出於進大學當時之興奮心情，在數學課所記得筆記來瀏覽，恰遇有同事井上博允助教授從傍窺視，說「寫得很整齊呀！」，這是大學入學後最初的筆記本之一頁；細心的筆跡，象徵著我青春的開始。自忖井上先生沒看第二頁，可說真僥倖。
第一頁開始寫著下面事項：
『
實數的性質
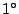.對於加法，乘法自成為一個體
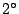.順序公理(省略)
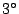.阿基米得公理
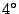.連續性公理(Weierstrass公理)
… 』
至今回想當時之情景，不由得浮現出教室內的新納文雄老師，他左手邊將垂髮撥上，笑容可恭地默默在黑板上書寫的情形，記得當天就寫了 10頁。我要是遇考試，不管題目怎麼出，自信還可如願解出，
但卻不知為什麼隨著老師抄寫黑板。這個筆記在學生寮 (宿舍)之木板床上，以悲悽之心情，翻閱至深夜無法入睡。
第二天，在校園內巧遇高中時的前輩，乃問以「大學的數學，真夠怪的」，前輩乃說「進了大學，不念《解析概論》-(即分析導論或稱高等微積分)是不可以的，且要對 ε,δ 能習慣」。於是用媽媽的朋友祝賀我考取大學的千圓，買了一本高木貞治著的《解析概論》(該書有中譯本，由葉能哲、賴漢卿合譯，名為《高等微積分》)，就開始啃，此乃我修習數學的第一部。
在高中時對於「數列的收斂」所授之「無限接近之事」乃改用「任意給定之正數 ε，與之對應的一正整數 n0而於
來決定」。在這種非常嚴密的敘述下，才算是數學，是當時所以領會到的記憶。
於是前輩所說的 ε,δ，到「連續的均勻性」之概念來想像時，也就能習慣了。ε,δ 是讀函數解析(即泛函分析)的基本事項，在感覺裏，這是與高中所讀的數學最不同之點，且此對自己也很有助益，這些都要謝謝我那位前輩先給與我的忠告。
- 2.有許多記憶的事象
當 ε,δ 已習慣後，才再記起大學入試前所讀的數學與大學中之數學，有很大不同；高中數學，在給與的題目中都以能「漂亮地」解出為主，所以入試前的數學，都想漂亮能解出的問題，是為數學問題之運用而生。這種淺見，認為數學所表現的問題，都要能漂亮解出來。因此對 ε,δ 也以為會出現這類問題。
回顧入試數學領域中，乘法公式只要記得幾個，則因式問題必能克服;二次方程式之根與係數的關係，要是能十分理解，一定能解決許多問題，心裏想只要利用很少的道具，就有許多收穫，乃是數學。所以在高中時之數學表現，都能享受數學說明的樂趣，說實在的，在問題集裏，分組取用就有此現象。比如討論二次方程式時，祇要記得根的公式，則不論什麼方程式，都能容易解出，就像導入虛數 i 來說，只要以一公式，便能擴展到複數的整個世界去，覺得自己學到了萬能的方法，這是一很深刻的記憶。
但來到大學的數學時，這種萬能的公式卻不復存在，於是開始注意到非記憶不可的事項太多了，就是最單純的一階常微分方程式 (當開始學習時的想法)，其形式就有 Bernoulli形，Riccati 形等之稱呼，而其解法則完全不同，同時非將此解法記到某程度不可，蓋因它無法導到簡易之解法。因有此情形，讀者諸君，在開始學習微分方程式論初期，大概會體會到「結果只取能解的方程式，而能解之方程式大概都很受限制吧!」這不過是我自己的經驗，隨意下的結論，但為加強工程方面之有用數學，則非記憶很多公式不可。工程學家是數學的使用者，數學家所開發出來的多彩多姿的道具，緊握在手中即可。
- 3.數學的奇妙
本稿開始，是介紹自己的筆記，這是屬解析(即分析)的講義。另有一種所謂「幾何」，是由谷山豐先生(年青早逝)講授，這是一門難以理解的課，他常以「n 維空間」為對象，如全班同學，最初是合成班，二年後要進到各自專門的院別，班裏同學得解散分發，而其系別名稱很多，乃由「n 維」所決定。但此時所學，到現在卻非常有用，這也可以說是擴展到很廣泛範圍的一門學問。其他如線性規劃，彈性矩陣分析，有限數學等，在工程學上也是極有用的應用技法，當時的筆記本甚有見效，乃是最高興的一件事。
學工程的人，決定自己專門方向後，在學數學的使用時，必須要認識數學的奇妙所在。雖然前述之微分方程，想到能解的畢竟有限，然而這些能解的微分方程式，卻說明了自然現象上，最適切而取用的情形。當然這也可能是在研究進展下，將解法形成定式化而已。在高中時，埋首於「漂亮」解，所能期待的也就是這種時期，即能具體的被應用於自然現象的事項。具有「圓對稱性」領域上之偏微分方程式，如波動方程式，熱傳導方程式等，幾乎全部之應用都適用於 Bessel微分方程式。同樣的 Laplace方程式 (表示著許多的自然現象)用空間之極坐標表現，如欲解此方程式 (可用變數分離法)，則其出現之一常微分方程式為 Legendre方程式。球形物之熱傳導或流動的分析，就是為這種方程式所約束，當你讀這一帶之東西時，還是會覺得數學具有萬能。
我的恩師渡邊茂先生，因具有很優秀之數學修養，很幸運地從研究院時代起，使我對數學的各部門有接觸的機會。在上述的情形，我對數學常會有下面三步驟之想法:
- 1.以為不易突破。
- 2.因要記的東西太多，帶著手冊 (公式、方法)那就大概夠了。
- 3.遇到大事情，就感到數學的偉大。
