甲、乙兩人玩丟擲銅幣賭博的遊戲,雙方約定,如果擲銅幣出現的是人頭,則甲付給乙兩元。如果出現的是梅花,則須再擲一次銅板;如果出現的仍是梅花,則須繼續擲,一直等到第一個人頭出現才停止。這時,甲要付給乙 2n 元,其中 n 為丟擲銅板的次數。
問:在遊戲之初,乙應該先付給甲多少錢,這個遊戲才算公平?
我們先來看個簡單的例子。如果丙、丁兩人也玩擲幣打賭的遊戲。他們的規則是:如果出現的是人頭,則丙付給丁 2 元;如果出現的是梅花,則丙就不付錢給丁。整個遊戲只須丟一次銅幣就要結束算帳。問:在遊戲之初,丁應該先付給丙多少錢,這個遊戲才算公平?丁在一次遊戲中有二分之一的機會可以得到兩元,有二分之一的機會得不到錢;因此,我們說,平均起來,丁可以從丙那裏得到
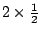
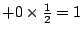 元。根據這些,我們認為公平的做法是丁在遊戲之初先付一塊錢給丙。 元。根據這些,我們認為公平的做法是丁在遊戲之初先付一塊錢給丙。
現在我們依照同樣的道理來處理原來的題目。我們知道,在遊戲結束的時候,乙可能得到 2 元,也可能得到 4元,8元,16元,……。他得到 2元的或然率是 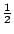 ,得到 4元的或然率是 ,得到 4元的或然率是 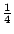 ,得到 8元的或然率是 ,得到 8元的或然率是 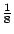 ,……。因此,平均說來,乙可以從甲那邊得到 ,……。因此,平均說來,乙可以從甲那邊得到
根據這個,我們是不是認為要乙先付「無限多」的錢給甲才算公平呢?
顯然的,耍乙先付「無限多」的錢給甲是件荒謬的事。首先,這個「無限多」的錢要如何解釋。好了,我們就姑且認為「無限多」的錢是指的比任意多還要多的錢。則明明乙只能從甲那邊得到有限多的錢,我們怎麼可以要乙先付無限多的錢給甲。
我們知道,耍乙付那個平均數給甲是有數學上的依據(大數法則),而且也符合直觀要求的。但是,該留意到的是,當著平均值不是一個數的時候,(譬如說是 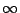 ),我們就不該把數學上的結果硬梆梆的壓到乙的身上。總結的說,要求乙在事先付一個數目來使得遊戲公平是辦不到的事。(St. Petersburg's paradox) ),我們就不該把數學上的結果硬梆梆的壓到乙的身上。總結的說,要求乙在事先付一個數目來使得遊戲公平是辦不到的事。(St. Petersburg's paradox)
|