海外學人相親記 (第 3 頁)

　1│2│3│4　

海外學人相親記（第 3 頁）

李宗元

首頁 | 搜尋

．原載於數學傳播第二卷第三期
．作者當時任教於中央數學系

‧註釋
‧對外搜尋關鍵字

退而求其次

這個標題可能會引起誤會。我的意思是，如果你把眼光稍為放低一點，能夠選中第一名或第二名就好的話，那麼你應該採取怎樣的手段?

很自然地，一開始你仍應按以前的辦法進行，自第r位起，等候第一個臨時第一名。但是如果等了一段時間，佳人尚未出現，你心裏便難免緊張起來:是不是第一名已成漏網之魚? (已經在最前面r-1位中出現了)。所以你應該自第s位(s>r)起，首次碰到臨時第一名或臨時第二名時，你都一把抓住，因為臨時第二名也可能會是實際第二名。我們也可以證明，最好的手段，就在這一類裏，不過我也不證明了。我再簡寫如下:

M_r,s:自第r位起，選擇臨時第一。自第s位起,(如果以前尚未選定)，選擇臨時第一或臨時第二

我們現在來算M_r,s的成功機率。符號如前。

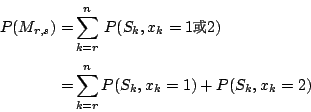$\begin{displaymath} \begin{eqalign} P(M_{r,s})=&\sum^n_{k=r}\,P(S_{k},x_k=1 \mbo... ...} 2)\\ =&\sum^n_{k=r}{P(S_k,x_k=1)+P(S_k,x_k=2)} \end{eqalign}\end{displaymath}$

(6)

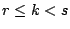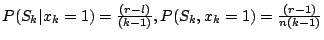(i) $r\leq k<s$ : $P(S_k\vert x_k=1)=\frac{(r-l)}{(k-1)}, P(S_k,x_k=1)=\frac{(r-1)}{n(k-1)}$ 。

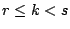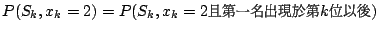(ii) $r\leq k<s$ : $P(S_k,x_k=2)=P(S_k,x_k=2 \mbox{{\fontfamily{cwM0}\fontseries{m}\selectfont \cha... ...0pt plus0.2pt minus0.1pt{\fontfamily{cwM1}\fontseries{m}\selectfont \char 40}})$ 。

(因為如果第k位是第二名，而第一名出現在先，則按照上述辦法，第k位根本不會被選到)。

現在

$\begin{displaymath} \begin{eqalign} P(x_k=2\mbox{\hskip 1.2pt plus0.4pt minus0.2... ...{m}\selectfont \char 40}}) &= \frac{(r-1)}{(k-1)} \end{eqalign}\end{displaymath}$

故

$\begin{eqnarray*} P(S_k,x_k=2)&=&\frac{r-1}{k-1}\cdot\frac{(n-1)-(k-1)}{n(n-1)}\\ &=&\frac{r-1}{n(k-1)}-\frac{r-1}{n(n-1)} \end{eqnarray*}$

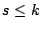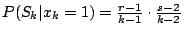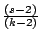(iii) $s\leq k$ : $P(S_k\vert x_k=1)=\frac{r-1}{k-1}\cdot\frac{s-2}{k-2}$ ，因為這時第k位要被選中，一定是a:前k-1位中最好的要在前r-1位裏，而且b:前k-1位中次好的要在前s-1位中。注意 $\frac{(s-2)}{(k-2)}$ 是P(b|a) 。所以

$\begin{displaymath} P(S_k,x_k=1)=\frac{1}{n}\cdot\frac{r-1}{k-1}\cdot\frac{s-2}{k-2} \end{displaymath}$

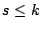(iv) $s\leq k$ :與(iii)中理由一樣，我們得到

$\begin{displaymath} P(S_k,x_k=2)=\frac{1}{n}\cdot\frac{r-1}{k-1}\cdot\frac{s-2}{k-2} \end{displaymath}$

把所有上面結果放進(6)式裏，我們就有

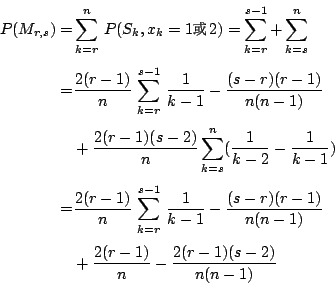$\begin{displaymath} \begin{eqalign} P(M_{r,s})=&\sum^n_{k=r}\,P(S_k,x_k=1\mbox{{... ...& +\frac{2(r-1)}{n}-\frac{2(r-1)(s-2)}{n(n-1)}\\ \end{eqalign}\end{displaymath}$

(7)

我們再討論，當 n 很大時，最好的 r 和 s（=r^*,s^*）以及 P(M_r^*,s^*) 該是多少。因為(7)式較複雜，最快的方法，就是將這個非連續變數的式子，用連續變數的式子來取代，（discrete 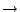$\rightarrow$ continous，這是一般應用數學中的慣技），然後再用微分的方法。這裏我只得向一般中學同學們作個道歉，這也是不得已的事。前一節裏的結果，你如用微分的方法，也可更快得到，至少可以省去了整頁的篇幅。

我們令

$\begin{displaymath} x=\frac{r}{n},\qquad y=\frac{s}{n} \end{displaymath}$

根據前面的經驗，當n很大時，r^*和s^*也應該很大。因此如果 (r,s)在(r^*,s^*)附近的話，r和s也都很大，所以

$\begin{displaymath} \sum^{s-1}_{k=r}\,\frac{1}{k-1}\approx\log{\frac{s}{r}}=\log{\frac{y}{x}} \end{displaymath}$

你若稍為觀察，可見(7)式右方與下式相近

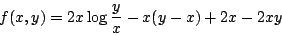$\begin{displaymath} f(x,y)=2x\log{\frac{y}{x}}-x(y-x)+2x-2xy \end{displaymath}$

(8)

現在我就當x,y為連續變數，求f(x,y)的最大點(x^*,y^*)。根據微分的方法，(x^*,y^*)應是下面兩式的解:

$\begin{displaymath} \frac{\partial f}{\partial x}=0,\quad \frac{\partial f}{\partial y}=0 \end{displaymath}$

計算這兩個偏微分，分別得到

$\begin{displaymath} -2x+3y=2\log{\frac{y}{x}},\quad \frac{2x}{y}=3x \end{displaymath}$

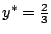由此我們得到 $y^*=\frac{2}{3}$ 以及

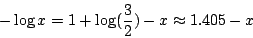$\begin{displaymath} -\log x=1+\log (\frac{3}{2})-x \approx 1.405 -x \end{displaymath}$

(9)

這是個「超越方程式」，x^*是(9)式在(0,1)間的解。x^*的近似值並不難求，見圖5。你如有個小型計算機,不消花多少時間,

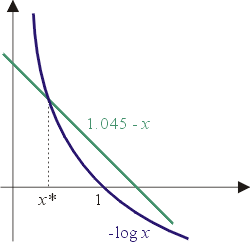
圖5

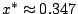就可以找出 $x^*\approx 0.347$ 。再從(8)和(9),你就得到

$\begin{displaymath} f(x^*,y^*)=x^*(2-x^*)\approx 0.574 \end{displaymath}$

所以我們新相親法的答案是

$\begin{displaymath} r^*\approx 0.347n,s^*\approx \frac{2}{3} n ,P(M_{r^*,s^*})\approx 0.574 \end{displaymath}$

你有超過一半以上的機會，可以選中第一名或第二名!這和隨意亂選一位的成功機會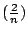 $(\frac{2}{n})$ ，真是天淵之別。你還堅持數學無用嗎?

　1│2│3│4　


	（若有指正、疑問……，可以在此留言或寫信給我們。）

EpisteMath (c) 2000 中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有

編輯：洪瑛

最後修改日期：4/26/2002