一般而言,數學是先有觀察與猜測(這個階段允許犯錯),然後才有試驗、修正與證明。數學絕不是突然 (out of the blue) 從天上掉下一個公式或定理,然後就要我們去證明。通常數學教科書所犯的毛病就是按「定義、定理、證明,等抽象方式來舖陳,這樣無法看到數學的發展過程。
為了證明(7)式,首先讓我們分析單純多邊形:
- (i)
最簡單的單純多邊形就是原子三角形 (atomic or primitive triangles),亦即除了三個頂點之外,三邊及內部皆不含格子點之三角形,見圖十五,其面積皆為
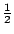 ,並且可用(7)式來計算: ,並且可用(7)式來計算:
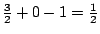 。因此,對於原子三角形,上述(7)式成立。 。因此,對於原子三角形,上述(7)式成立。
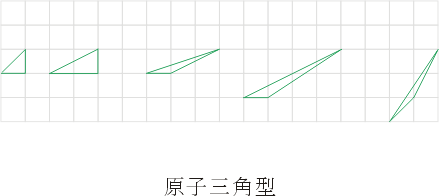
圖十五:原子三角形
|
- (ii)
其次,我們觀察到,對於任意的單純多邊形都可以先分割成三角形(即三角形化),再進一步分割成原子三角形之組合(這叫做原子化),見圖十六。
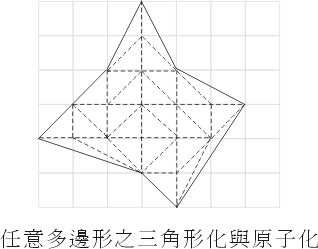
圖十六:任意多邊形之三角化與原子化
|
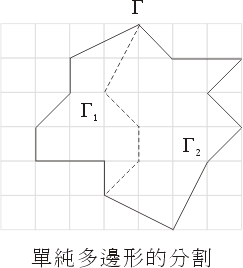
圖十七:單純多邊形的分割
|
- (iii)
最後考慮任何單純多邊形 Γ 將它分割成兩個單純多邊形
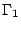 與 與 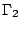 ,見圖十七。設 Γ 有 b 個邊界點、i 個內點,並且 ,見圖十七。設 Γ 有 b 個邊界點、i 個內點,並且 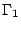 與 與 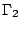 分別有 b1 個與 b2 個邊界點、有 i1 個與 i2 個內點。再設 分別有 b1 個與 b2 個邊界點、有 i1 個與 i2 個內點。再設 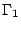 與 與 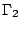 有 b3 個共同的邊界點,則 有 b3 個共同的邊界點,則
所以
因此,公式(7)在分割下,具有加性 (additivity)。
上述三個步驟綜合起來,我們就證明了(7)式,一旦猜測有了證明,就成為定理。
- 定理一:Pick 定理,1899年
- 設 Γ 為平面上以格子點為頂點之單純多邊形,則其面積為
其中 b 為邊界上的格子點數,i 為內部的格子點數。(8)式叫做 Pick 公式。
在上述證明中,單純多邊形經過原子化後,成為一個連通的平面圖枝 (a connected plane graph)。著名的尤拉 (Euler) 公式告訴我們,對於任何連通的平面圖枝(不限於格子點圖枝)恆有:
其中 V 表示圖枝的頂點 (vertices) 個數(即 V=b+i),E 表示稜線 (edges) 的個數,F 表示平面被圖枝分割所成的塊數(其中最外的一塊是無界的)。例如,在圖十六中,V=20,E=49,F=31。
因為每一個原子三角形的面積為 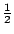 ,並且總共有 F-1 個,所以原來單純多邊形的面積為: ,並且總共有 F-1 個,所以原來單純多邊形的面積為:
由尤拉公式與 V=b+i 得到:
再由 Pick 公式,可知:
於是我們得到稜線的個數為:
事實上,這個公式對於一般連通的三角形化的平面圖枝(不限於格子點圖枝)都成立。
- 定理二:(稜線定理,Edge Theorem)
- 對於任意連通的三角形化的平面圖枝,其稜線的個數恆為
其中 b 與 i 分別表示圖枝邊界上的頂點數與內部的頂點數。
- 證明:
我們分成三個步驟:
- (i)最簡單的情形是 b=3,i=0,圖枝只含一個三角形,此時 E=3,故公式(13)成立。
- (ii)若在三角形的內部增加一個頂點,則 E 增加 3。此時(13)式也成立。
- (iii)假設一個連通的三角形化的平面圖枝滿足(13)式(即 E=2b+3i-3),今在其外部增加一個新的邊界頂點,使得原來圖枝的邊界頂點有 m 個變成內部頂點(m 可能等於 0),則 E 增加 m+2。於是由 E=2b+3i-3 得:
E+m+2=2(b+1-m)+3(i+m)-3
換言之,對於新的圖枝而言,(13)式仍然成立。按數學歸納法,我們就證明了(13)式。
由稜線定理與尤拉公式,我們也可以推導出 Pick 定理,這就是下面要介紹的 Pick 定理之第二種證法:
根據 V=b+i, E=3i+2b-3, V-E+F=2,以及面積
 ,立即可算得: ,立即可算得:
反過來,由 Pick 定理與稜線定理也可以推導出尤拉公式(見參考資料7)。
由 Pick 定理知,以格子點為頂點之多邊形,其面積必為有理數,但是正三角形的面積為無理數,所以我們有了
- 推論:
以格子點為頂點之正三角形不存在。
事實上,我們可以證得一般結果,如下:
- 定理三:
正方形是唯一以格子點為頂點之正多邊形。
|