黎曼幾何把幾何局部化，但我們不能永遠只在一個小區域裡頭，所以局部化之後又要整體化，又要把它擴充到全空間。而在這個整體化的擴充當中，最要緊的就是拓樸學。只要我們不把一個圖形扯破，那麼就有些幾何性質雖經過放大、縮小等很大的變換，也不會改變，例如虧格 (genus) 的性質。比方說我們在一個二次的曲面上挖兩個洞（見圖六），那麼它的虧格就等於 2。虧格也可以等於 3、4……，或者像美國的甜甜圈只有一個洞，虧格就是 1。即虧格等於洞的個數，這個數目是把曲面放大縮小之後仍舊不變的，這是拓樸不變式的一個例子。

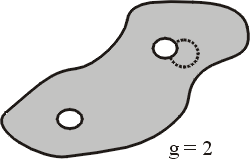
圖六

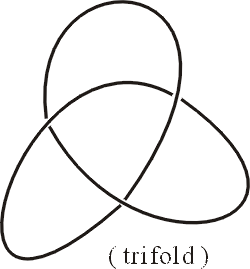
圖七

另外一個例子是有關於結 (knot)。如圖七，這是一個三維空間中封閉的曲線，沒有辦法把它解開成一圓周，這就是所謂的結。不要把這想成幾何學家沒有事在玩的東西，在應用上，這有非常重要的意義。剛才說過，物理上的空間是四維的，如果再加上電磁場，就成了五維的空間。馬克士威方程式中，底空間是一個四維的流形，在那上頭的每一點都突出去一條一維的空間（矢量叢）。這一維的空間，在物理上必須是封閉的，所以是一個圓周，數學家稱此為圓周叢 (circle bundles) 也就是說，底空間是四維，每一點又有一個圓周，所以整個空間就是五維的。但是這並不是一個任意的五維空間，它必須滿足這樣特別的一個幾何結構。利用這個觀念，馬克士威方程就可寫成下面這樣簡單的形式：

其中 F 是這個圓周叢的一個聯絡的曲率，這曲率是一個二次微分式，d 是代表此微分式的外微分，dF=0 就是說這個二次微分式是封閉的。

另外一個方程式是 δ， ，即所謂餘微分(codifferential)。在一般的電磁學書上，是用一組方程來表現馬克士威方程。現在由於數學或幾何的發展，不但把一組方程式簡化，而且可由這化簡的方程式去推得數學、幾何、物理上的結論，並不一定要回來把方程式全展開才可獲得相同的結論。所以這觀念上的發展，的確使得科學進步。如果大家有興趣，可試著去證明這組方程和平常我們所見的馬克士威方程是一樣的。

圖八