歐幾里得幾何之後，第二個重要的發展是坐標幾何。這是法國哲學家、數學家笛卡兒（1596∼1650年），對於研究幾何，引進了坐標的概念，因此可用解析的方法來處理幾何的問題。坐標就是說：假使在 X-Y 平面上，有兩個軸：X 軸和 Y 軸，那麼一個點的兩個 X、Y 坐標，就分別以如圖四中的兩個相對應的度量來表示。

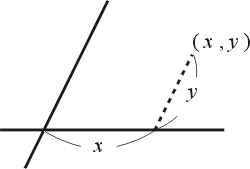
圖四

因此幾何的討論可用解析方法，即：

這樣的發展不但使幾何問題的處理容易些，更有其重大的意義：

一、解析之後，使可研究的圖形的範圍擴大，除了直線的一次方程式， 或者圓周的二次方程式，我們還可以取任意的方程式 f(x,y)=0， 討論所有點它的坐標 (x,y) 適合這樣方程式的軌跡。 因此許多用幾何的方法很難處理的曲線，在解析化之後， 都可從表示它的方程式中得到有關的幾何性質。

二、研究的圖形不再局限在二維的平面上，可推廣至高維的空間。 世界上的事情，如果只用二維的平面，往往不足以表示， 需要取更多的坐標。例如我們所在的空間是三維，有 x、y、z 三個度量。 假使要用幾何來表示物理的問題，那麼三個度量之外，尚須加一個時間 t， 所以物理的空間就變成了四維的空間；不但如此，假使有一點在三維空間運動，那麼除了需要 (x,y,z) 來表示點的位置， 還需要這三坐標對時間的微分來表示它的速率， 即 ( )， 這就成了六維空間。所以種種的情形都指示我們有必要考慮更高維的空間， 來表示自然的現象。

解析幾何把幾何研究的範圍大大地擴大了，而科學發展的基本現象， 就是要擴大研究的範圍，了解更多的情形。笛卡兒的解析幾何， 便達到了這個目的，使幾何學邁入一個新的階段。