| |
重覆且獨立地丟一個公正的銅板,這叫做 Bernoulli 試驗。令 An 表示第 n 次出現正面的事件,則 (An) 為一列獨立的事件並且
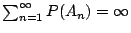 。由 Borel-Cantelli 補題知 。由 Borel-Cantelli 補題知
P(An, i.o.)=1
亦即不時地 (infinitely often, i.o.) 出現正面的機率為 1。從而,至少出現一次正面的機率也是 1。
今考慮每一次丟銅板出現正面的機率皆不同,令其為 p1,p2,p3,…,這叫做 Poisson 試驗。我們要問:在什麼條件下,至少出現一次正面的機率為 1?
顯然,由 Borel-Cantelli 補題知,若
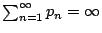 ,則至少出現一次正面的機率為 1。如果我們假設 ,則至少出現一次正面的機率為 1。如果我們假設 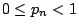 ,則反過來也成立。因為 ,則反過來也成立。因為
這最後一步需要用到 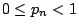 的條件。 的條件。
-
- 定理:
在 Poisson 試驗之下,若
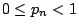 ,則下列三個敘述等價: ,則下列三個敘述等價:
- (i) P( 不時地出現正面 )=1,
- (ii)
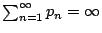 , ,
- (iii) P( 至少出現一次正面 )= 1。
特別地,取
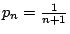 ,則 ,則
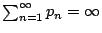 。於是 。於是
這恰是 Huygens 級數:
順便一提,在機率論中,要舉一個期望值不存在的隨機變數,
最簡單的辦法是考慮隨機變數 X,取值
則期望值為
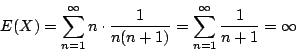 |
(14) |
這個隨機變數 X,出現於下面的機率問題。考慮一個甕 (Urn),
裝有一個白球與一個黑球。作隨機實驗如下:
- 任意取出一球。如果是白球,則終止實驗。如果是黑球,則放回,
並且再加一個黑球到甕裡。然後繼續從甕中任意取出一球。
- 不斷地重複(i)的步驟。
一直等到取出白球為止,試求取球次數的期望值。
上述隨機實驗的樣本空間為
每一樣本點的機率為
定義取球次數的隨機變數 X 為
於是 X 的期望值就是(14)式。
下面我們再看一個 Huygens 級數自然地出現的機率問題。
考慮一個隨機變數 X,代表玉皇大帝提供給人間的命運。假設人們排成一隊,
從時刻 0,1,2,… 一個接著一個來抽取命運,得到隨機樣本
X0,X1,…,Xn,…,它們獨立且同佈 (i.i.d.)。X0 代表某甲的壞運,
X1,X2,… 代表甲周圍親友的壞運。從心理的觀點來看,甲發生不幸後,
要等到周圍有人發生更大的不幸才得到安慰。亦即諺語所說的「壞運永不會變成好運,直到更壞的事情發生」(Bad is never good until worse happens)。如果我們用
來代表甲等待至得到安慰的等待時間,則 P(N>k) 表示在隨機變數
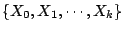 中,X0 是最大項。由對稱性 (i.i.d.) 可知 中,X0 是最大項。由對稱性 (i.i.d.) 可知
於是
我們稱隨機變數 N 具有Huygens分佈,它的期望值 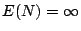 。因此,平均起來甲要等待無窮長的時間才得到安慰。這叫做「壞運的持久性」或「壞運的詭論」
(the ill-luck paradox)。 。因此,平均起來甲要等待無窮長的時間才得到安慰。這叫做「壞運的持久性」或「壞運的詭論」
(the ill-luck paradox)。
最後我們介紹一個跟連分數 (continued fractions) 有關的例子。取機率空間 (
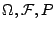 ) 為 Lebesgue 空間,亦即 ) 為 Lebesgue 空間,亦即
![$w=(0,1], \mathcal{F}$](img70.gif) 為 (0,1] 中的 Lebesgue 可測集全體,P 為 Lebesgue 測度。對於每一個 為 (0,1] 中的 Lebesgue 可測集全體,P 為 Lebesgue 測度。對於每一個
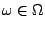 ,作連分數展開 ,作連分數展開
定義隨機變數
則每一個 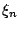 皆取值 1,2,3, 皆取值 1,2,3, 並且 並且
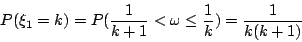 |
(15) |
因此,隨機變數 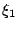 依從 Huygens 分佈。在這個模型之下,還可以證得許多美妙的結果,請參考 Kac [2]與 Barone & Novikoff [3]。
事實上,這是 Borel 開拓機率論的一個重要特例。 依從 Huygens 分佈。在這個模型之下,還可以證得許多美妙的結果,請參考 Kac [2]與 Barone & Novikoff [3]。
事實上,這是 Borel 開拓機率論的一個重要特例。
|
|
|