|
6. 推廣到三維空間:Gauss 定理與 Stokes 定理 |
抓住了 Green 公式的形式與內涵,要推廣到三維空間就不難了。首先令
表示空間中的一個向量場 (Vector field),即定義在空間中某領域的一個向量值函數。
- 定義:
-
分別叫做向量場 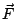 的散度與旋度。 的散度與旋度。
其次我們注意到,平面領域 Ω 可以有兩個方向的推廣:一個是空間中的可定向 (Orientable) 曲面 S(Möbius帶子就不是可定向曲面),參見圖16;另一個是空間中的一塊立體領域 V,參見圖17。
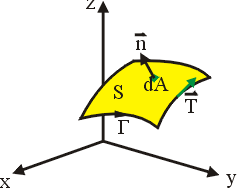
圖16
|
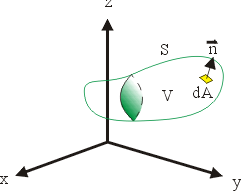
圖17
|
在(19)式中,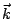 是 Ω 的向外單位法向量;當 Ω 改為空間曲面 S 時, 是 Ω 的向外單位法向量;當 Ω 改為空間曲面 S 時,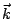 就應該改為 S 的向外單位向量 就應該改為 S 的向外單位向量 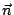 。 。
我們可以證明
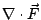 與 與
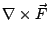 跟二維的情形有類似的解釋。 跟二維的情形有類似的解釋。
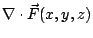 表示單位時間單位體積流體在點 表示單位時間單位體積流體在點 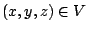 的流出通量, 的流出通量,
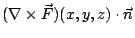 表示單位時間單位體積流體在點 表示單位時間單位體積流體在點 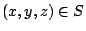 的循環量。從而(19)與(20)兩式就推廣為: 的循環量。從而(19)與(20)兩式就推廣為:
- 定理4: (Gauss 定理,又叫做散度定理,1839年)
- 設向量場
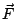 的分量 P,Q,R 及其一階偏導函數皆為連續函數,則 的分量 P,Q,R 及其一階偏導函數皆為連續函數,則
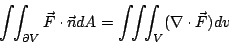 |
(31) |
其中 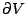 為圍成 V 之封閉曲面,dV 表示無窮小的體積元。 為圍成 V 之封閉曲面,dV 表示無窮小的體積元。
- 定理5: (Stokes 定理,又叫做旋度定理,1854年)
- 在與定理4相同的假設下,我們有
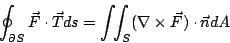 |
(32) |
參見圖16。
在上述中,(31)式與(32)式分別將曲面積分與三重積分,線積分與曲面積分連結起來。若採用直角坐標系來表達,它們分別就是
以及
這一切可以再推廣到 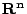 的可定向 k 維可微分子流形 的可定向 k 維可微分子流形
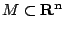 ,用微分式的積分與外微分理論,統合成為廣義的 Stokes 定理: ,用微分式的積分與外微分理論,統合成為廣義的 Stokes 定理:
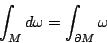 |
(34) |
其中 ω 為 k-1 型微分式。這是微積分學根本定理最本質的形式。
|