.丘成桐先生80年11月4日於中正大學應數所之演講,原載於數學傳播第十五卷第四期
丘成桐先生演講
丘成桐
紀錄:賴玲淑;劉榮彰
|
|
.丘成桐先生80年11月4日於中正大學應數所之演講,原載於數學傳播第十五卷第四期 | ||
|
Laplacian 算子對應譜的最近發展
丘成桐先生演講 丘成桐
|
|
此篇文章主要是探討譜與區域的對應關係。首先介紹何謂 Laplacian 算子,所謂 Laplacian 算子在一維空間是定義為
一開始,先看簡單的一維空間, 通常在一維的 Laplacian 算子的譜的問題可由弦振動來解釋之, 固定兩端點不動的均勻弦(密度 而由此 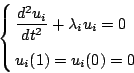
方程式,每任意特徵值 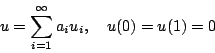
若此弦的密度 ρ 不均勻,那上述的方程要修正為 而在研究一維弦振動中有一重要性質,就是 Sturm-Liouville 性質:
但此性質在二維空間以上就不存在了,所以在研究二維空間的問題比較困難,跟一維空間不同。
綜合上述,給定弦本身的密度 ρ,可以決定一組譜
How to hear the shape of a drum?
那就是說,鼓可視為一個二維的有界區域 (domain),
所謂鼓的形狀,就是相對於區域的幾何性質,
這個問題就是怎麼樣從打鼓的音調聽出鼓的形狀。同樣的問題在一維空間的問題比較簡單,
因為整個 potential 可以寫下來,二維空間以上就比較麻煩,我們考慮的方程式為
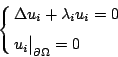
其中
而
但此問題還未被完全瞭解,例如: 其中 M 是一個流形 (Manifold) 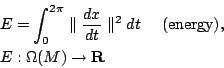
在此考慮 而加入
現在進入主要的問題:
基本上 wave mechanical approach 可用 kernel mechanical 來看,即考慮
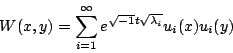
的形式,這可解出 wave equation,且滿足
|
對外搜尋關鍵字: .Laplacian算子 |
|
|
|
|
(若有指正、疑問……,可以在此 留言 或 寫信 給我們。) |
|
|
|
EpisteMath (c) 2000 中央研究院數學所、台大數學系 各網頁文章內容之著作權為原著作人所有 |
| 編輯:廖俊旻 / 校對:黃怡碧 / 繪圖:簡立欣 | 最後修改日期:4/26/2002 |