在談水珠反射之前,我們假設:
- 水珠是球形的。
- 光速極快,光線在水珠內的時間可以不計。
- 太陽光互相平行。
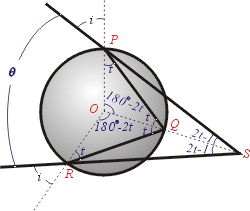
最基本的彩虹是在水珠中,經過一次反射形成的(見圖2),
試想光線由 P 點射入水珠,入射角為 i。P 點(或水珠面上任一點)的法線,
通過球心 O。折射線的折射角為 t 在 Q 點被反射,
反射線又在 R 點遇到水珠面,而穿出水珠面,產生一條折射線,
這折射線比原來的的入射線弱,因為每次光線遇到介面時,
都有一部份反射,另一些折射(見圖3)。
圖二
|
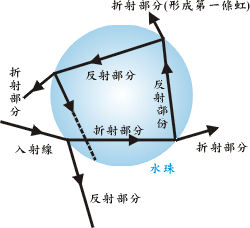
圖三
|
在 P 點的入射線和 R 點的折射線間的夾角,可以應用反射律、折射律及幾何學來求它,由水珠的球心 O 作三角形 PQO 和 RQO(見圖2),它們都是等腰三角形,因為 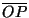 , ,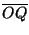 和 和 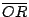 都是球半徑,又根據反射律, 都是球半徑,又根據反射律,
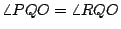 ,所以兩個三角形全等。其中頂點在球上的角就都等於 t,如果延長入射線和最後的折射線,交於 S,則其夾角 θ 就等於 ,所以兩個三角形全等。其中頂點在球上的角就都等於 t,如果延長入射線和最後的折射線,交於 S,則其夾角 θ 就等於
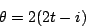 |
(2) |
這夾角和半徑(水珠的大小)無關。
現在假如有一束平行的太陽光,由水球上的不同點射入水珠,入射角當然也不同。根據反射律和折射律, 它們的路徑可以圖4 表示。經過球心的入射線,反射後還是它自己,而形成一條軸,由軸上方射入的光線,射出時在軸下方,但是並不是每個角度的反射線都能折射出去,入射線和最後的折射線的夾角有個最大值 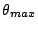 。圖4 顯示接近角 。圖4 顯示接近角 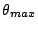 的反射線有集中的趨勢,於是在這個角附近造成特別強的反射光,就是這些集中的反射線造成了彩虹。 的反射線有集中的趨勢,於是在這個角附近造成特別強的反射光,就是這些集中的反射線造成了彩虹。
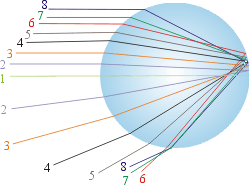
圖四
|
為了求 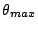 ,我們讓 θ 對 i 的微分為 0。別忘了 i 也是 j 的函數,所以當 ,我們讓 θ 對 i 的微分為 0。別忘了 i 也是 j 的函數,所以當
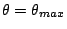 時, 時,
或
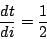 |
(3) |
把(1)對 i 微分,得到
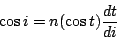 |
(4) |
將(3)代入(4),然後平方得到
利用
產生了
以 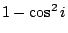 代替 代替 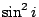 然後化簡成 然後化簡成
解 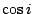 ,得 ,得 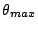 時, 時,
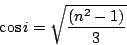 |
(5) |
由此式,用我們下一節的算法,可以算出 n 和 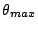
|