相異代表系古今談 (第 4 頁)

匈牙利算法彌補了何氏定理計算上的困難,相輔相成為一套完美理論。從這為出發點,有幾個發展方向,它們並不是互相獨立,而是互相參考,互補有無。我們列舉五個方向,略述大概。

有關(甲)這方向是計算機算法的課題。原來匈牙利算法所需的時間是O(n³), 其中n是頂點數,理論上是所謂的多項式算法(polynomial algorithm),比起 O(2ⁿ)的算法好上天,但精益求精,真正實際將這算法寫為程式時, 還希望能更快更省時,基於這個原則, Hopcroft和Karp發展出一個O(n^2.5)的算法。

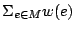(乙)是一個自然的推廣，在原來的二分圖網G=(X,Y,E)上，如果每邊 e對應一個正實數w(e)，原來問題的一個自然推廣是：求一對集M使得 $\Sigma_{e\in M}w(e)$ 值極大。在w(e)=1的情況，相當於求對集M使|M| 為極大,就是原問題。在婚姻問題裏，如果將w(e)視為媒婆綴合一對良緣收到的紅包，分權二分圖網對集問題就相當於媒婆想辦法拉紅線賺取最多紅包總錢數的問題。將原來匈牙利算法適當的修改，加入權數，可以成功的解決這問題；這方法的精神實在就是線性規劃中 primaldual simplex 方法的起源, 往後這方法被佛兒克森、艾德模斯等人一再的用到其他問題上。

我們一開始就已經說過,在冕哥看來,二分圖網對集是他研究圖網連通性的特例；把冕哥的理論發揮到極至的是福特 (Ford) 和佛兒克森，他們的最大流最小截 (maximum flow minimun cut) 理論，是這些理論的一個高潮，將相異代表系、柯尼哥及亞哥法利定理、冕哥定理、笛兒臥斯有關偏序集合鏈分解定理 $\cdots\cdots$ 種種紛雜的理論都納入一個體系之下，有一套完整的說法，在二十年後的今天看來，這樣的一統大業仍是十分偉大的。

我們在講匈牙利方法時曾敘述貝爾齊定理，這定理不只對二分圖網成立，對一般圖網都對，但是匈牙利方法卻不適用到一般的圖網，原因何在呢？現在讓我們看一個例子。

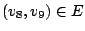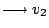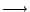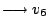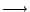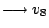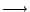根據原來的講法,這表示不存在M-可擴張路徑,但是事實上 (v₁,v₂,v₃,v₄,v₅, v₆, v₈,v₉ ,v₇, v₁₀,)是一條M-可擴張路徑。造成這樣的一個主要原因是在第4層的兩個頂點v₈和 v₉相鄰, 這在二分圖網不可能發生。就因為 $(v_8,v_9)\in E$ ,所以在 C=(v₃,v₅,v₈, v₉,v₆,v₃)這個迴路中, 我們可以任意調節使得這個迴路的任一點都相當於正頂點, 而可以接出一個負頂點,例如對於v₅(負號), 若想成v₁(正) $\longrightarrow v_2$ (負) $\longrightarrow$ v₃(正) $\longrightarrow v_6$ (負) $\longrightarrow$ v₉(正) $\longrightarrow v_8$ (原來正,看成負) $\longrightarrow$ v₅(原來負,看成正),同理 v₃,v₅,v₈,v₉,v₆ 都可以視為正頂點, 在艾德模斯看來,這個迴路 C 像一朵漂亮的花 (Blossom), 他的做法是將這朵花看成一點,也就是把 C 的所有頂點縮成一點,再繼續原來的做法, 直到找出一條 M-可擴張路徑或證明不存在為止, 這個過程中可能一再重複碰到將花朵縮成一點這件事。以上就是艾德模斯「花朵算法」(Blossom algorithm)的簡單說法。這個算法也可以推廣到頂點加權的問題。

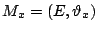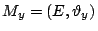最後,將二分圖網求最大對集的問題看成兩擬陣相交問題,可回到例6。如果G=(X, Y,E)是一個二分圖網,則可以定義兩個擬陣 $M_x=(E,\vartheta _x)$ 及 $M_y=(E,\vartheta _y)$ 。其中

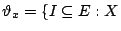$\vartheta _x=\{I\subseteq E: X$ 的每一頂點最多是I中一條邊的端點 },
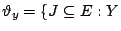$\vartheta _y=\{J\subseteq E: Y$ 的每一頂點最多是J中一條邊的端點 }。

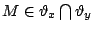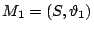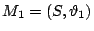不難驗證M_x和M_y是定義在E上的兩個擬陣,而且M是G的一個對集若且維若 $M\in \vartheta _x\bigcap \vartheta _y$ ,所以求G中最大對集等於求最大 M_x及M_y獨立集。一般來說,如果給兩個定義在同一集合S上的擬陣 $M_1=(S,\vartheta _1)$ 及 $M_2=(S,\vartheta _2)$ ,也可以問同樣的問題, 而這問題的解法將以前網路流的道理用到極致,是一個很成功的推廣。

綜而言之,從1930年代的相異代表系到兩擬陣相交問題, 其精神和技巧是匈牙利方法的一再延伸和擴張。這一路研究，在近二十年來是很突出令人矚目的。

: 1.王子俠〈相異代表系統簡介〉，《數學傳播》第四卷第四期(69年12月)第8-12頁,。
: 2.Liu,《Introduction to Combinatorial Mathematics》, New York, McGraw-Hill, 1968.
: 3.Mirsky,《Transversal Theory》, New York, Academic Press, 1971.
: 4.Welsh,《Matroid Theory》,New York, Academic Press, 1976.


	（若有指正、疑問……，可以在此留言或寫信給我們。）