| |
|
��{�� x3+y3=z3 ���Ĥ@�ر��p |
�ڭ̥��ޤJ�P�l (congruence) �������C
�Y n �O�Y�ӥ���ơAm1�P m2 �O��ơA�p�G n �i�H�㰣 m1 - m2 �A
�ڭ̻��Gm1 �P m2�A
�b�� n ���U�P�l (mi is congruent to m2 modulo n)�A
�O��
 �C
�ڭ̤������ӦP�l���� m1 �P m2 �ݦ��P�@�ӡu�ơv�A
�]���b�� n ���U�A�ڭ̱o��@�ӥu�� n �ӡu�ơv���ƨt�A
{ 0,1,�K,n-1 }�C�Ҧp�A�b�� 3 ���U�A �C
�ڭ̤������ӦP�l���� m1 �P m2 �ݦ��P�@�ӡu�ơv�A
�]���b�� n ���U�A�ڭ̱o��@�ӥu�� n �ӡu�ơv���ƨt�A
{ 0,1,�K,n-1 }�C�Ҧp�A�b�� 3 ���U�A
�o�ӷs�ƨt���B��k�h�A�[�B��B���A�P��ƨt���ۦ��C
�p�G p �O�@�ӽ�ơA
�ƨt {0,1,�K,p-1 } �Ʀ��٦����k�]���Ƥ��i���s�^�F
�]���A�o�Ӽƨt�i�H�����z�Ƥ@�˶i��[�B��B���B���C
�z�Ѧ�b�A��Ū�̦ۤw�ҩ�
��9
�C
�Q�ΦP�l�������A�ڭ̭p�� 232 ���Ӧ�ơC�A�p�G�� 232 ���}�ӨD��Ӧ�ơA�i��T�M�i�šA��k�o���ȱo���y�C�Ъ`�N�A�Y
�h
�]���A�b�� 10 ���U
�o�G232 ���Ӧ�ƬO 6�C
�{�b�ڭ̤��Ф@�Ӭ�s Fermat ���D�������C
�p�G Fermat ���D��� n �O�����A�]�N�O�A�s�b������s����� x,y,z�A����
xn + yn = zn�A�Ҽ{�o�Ӱ��D�Gn �P xyz �|���|����H
�p�G�b�H�W���ΤU�An �P xyz ���w���|����A�ڭ̴N���AFermat ��{���A
xn + yn = zn ���Ĥ@�ر��p���ߡC
�k��k�ƾǮa Sophie Germain�A
�]1776��1831�~�^�ҩ��G�Y p �P 2p+1 ���O��ơA
�h Fermat ��{��
xp + yp = zp ���Ĥ@�ر��p���ߡC
Legendre ���s Germain ����k�A�ҩ��G�Y p �O��ơA
�B 4p+1, 8p+1, 10p+1, 14p+1, 16p+1 �ܤ֦��@�ӬO��ơA
�h Fermat ��{�����Ĥ@�ر��p���ߡC
�ثe���D���O�A�Y p �O�_��ơA�B
p<3 x 109�A
�h Fermat ��{��
xp + yp = zp ���Ĥ@�ر��p���ߡC�]������� 7 �`�^
-
- �w�z 3
Fermat ��{��
x3 + y3 = z3 ���Ĥ@�ر��p���ߡC
���y�ܻ��A�p�G x1, y1, z1 �O������s����ƨåB����
x13 + y13 = z13�C
x13 + y13 = z13�A�h
 �C �C
- �Q�סG
�\�h�ҾڨϤH�۫H�AFermat ���T����ҩ��A
x3 + y3 = z3
�S��������s����ƸѡA
Fermat ��o�Ӱ��D�ܦ����Ǿ�ƥi�H�g�� x2 + 3 y2 �������C
Euler �Q�n��o�өw�z���ҩ��g�U�ӡA���O Euler �g�o�ä�����C
���㪺�ҩ��Ь� G.H Hardy and E.M. Wright,�mAn introduction to the theory of numbers�n�A�� 193-197 ���C
����u�ѨM Fermat��{���A
x3 + y3 = z3 ���������ΡC���� Germain �w�z�A�Ь� H.M. Edwards,�mFermat's last theorem �n�� 61-65���C
�H�U�n���X�w�z 3 ���t�@���ҩ��C
�o���ҩ��D�`�c�ơA�γo�Ӥ�k���ҩ��w�z 3 ²���O�M���z���C
���O�A�q�o���ҩ��o�i�H�ݥX�Q�E�@����s Fermat ���D����k�C
�ƹ�W�A��o���ҩ��y�[�ק�A�i�H�ҩ� Kummer ���@�өw�z�G
�Y p �O�@�ӳW�h��ơA�h Fermat ��{��
xp + yp = zp ���Ĥ@�ر��p���ߡ]�����W�h��ơA�Ьݥ���� 6 �`�C�^�C
�O x, y, z �O����B������s����ơA���� x3+y3=z3�A
�ڭ̭n�ҩ�
 �C
�������] x �P y �O�_�ơAz �O���ơ]�_�h�A���s�R�W�A�åB�����^�C
�O �C
�������] x �P y �O�_�ơAz �O���ơ]�_�h�A���s�R�W�A�åB�����^�C
�O
 �C
�Ъ`�N�G �C
�Ъ`�N�G
�@�Ӳ��Q�Ѷ}���D�N�G�p�G�Az-y,  , ,
 ����A�h�] ����A�h�]
�O�����ߤ�ơAz-y,  , ,
 �Z���]�O�����ߤ�ơH �Z���]�O�����ߤ�ơH
���D�O�A �����O�ӽƼơA
���i���ܦ���ƪ��ߤ�H�o�Ӱ��D�����ѨM�C�ڭ̥i�H��u��ơv���������s�C
���� �����O�ӽƼơA
���i���ܦ���ƪ��ߤ�H�o�Ӱ��D�����ѨM�C�ڭ̥i�H��u��ơv���������s�C
���� 
 �s���T�������� (cyclotomic field)�A
�T�������骺�����i�H�@�[�B��B���B���]���Ƥ����s�^�A�T��������O���z�ƪ����s�C
�T�������餧�����u��ơv�N�O �s���T�������� (cyclotomic field)�A
�T�������骺�����i�H�@�[�B��B���B���]���Ƥ����s�^�A�T��������O���z�ƪ����s�C
�T�������餧�����u��ơv�N�O
![$\mathbf{Z}[\omega]$](img46.gif) �������s���T�������� (cyclotomic integers)�C
�ҥH�W�z�����D�u���L�O�A �������s���T�������� (cyclotomic integers)�C
�ҥH�W�z�����D�u���L�O�A �ण��g���Y�@�ӤT�������ƪ��ߤ�H
�p�G �i �P �b ���O�T�������ƥB �ण��g���Y�@�ӤT�������ƪ��ߤ�H
�p�G �i �P �b ���O�T�������ƥB  �A
�ڭ̻� �i �㰣 �b�A�p�G �A
�ڭ̻� �i �㰣 �b�A�p�G
 �]�O�T�������ơ]
�]�O�T�������ơ]
 ���M�b ���M�b
 �����C��G�H�^�C
�]���b�T�������Ƥ����]�i�Q�צP�l���Y�G
�]���ڭ̥i�H�W�w�A �����C��G�H�^�C
�]���b�T�������Ƥ����]�i�Q�צP�l���Y�G
�]���ڭ̥i�H�W�w�A
 ���R�n����O �i �㰣
���R�n����O �i �㰣
 �C
�@�Ӥ����� �i �s���i�f���� (invertible element)�A�p�G �C
�@�Ӥ����� �i �s���i�f���� (invertible element)�A�p�G  �]�O�����ơ] �]�O�����ơ] ���M�b ���M�b
 �����^�A�Y �����^�A�Y
 �A�h �A�h
![$\mathbf{Z}[\omega]$](img46.gif) �����i�f�����u�� �����i�f�����u�� 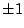 , , , , �C�]��G�H�^ �C�]��G�H�^
�@�ӫD�s�������� �i �s�����i������ (irreducible element)�A
�p�G �b �O�����ƥB  �A
�b ��㰣 �i�A�h �b �� �A
�b ��㰣 �i�A�h �b ��
 �ܤ֦��@�ӬO�i�f�����C
���i�������O��ƪ����s�C �ܤ֦��@�ӬO�i�f�����C
���i�������O��ƪ����s�C
���ФF�����ơB�i�f�����B���i����������A�ڭ̴N�i�H�Q��
![$\mathbf{Z}[\omega]$](img46.gif) ���]�Ƥ��Ѱ��D�C�ڭ̧� ���]�Ƥ��Ѱ��D�C�ڭ̧�
![$\mathbf{Z}[\omega]$](img46.gif) ���X�Ӱʽ�C�|�p�U�G ���X�Ӱʽ�C�|�p�U�G
- (1)
![$\mathbf{Z}[\omega]$](img46.gif) �㦳�ߤ@���ѩʽ�C���骺���A
(i) �㦳�ߤ@���ѩʽ�C���骺���A
(i)
![$\mathbf{Z}[\omega]$](img46.gif) �����N���� �a�A
�Y �����N���� �a�A
�Y  �A�a �]���O�i�f�����A
�h �a �i�g�� �A�a �]���O�i�f�����A
�h �a �i�g��
 �������A �������A
 �O���i�������A
(ii) �p�G �O���i�������A
(ii) �p�G

 �A�䤤 �A�䤤  �P �P  ���O���i�������A
�h n=m�A�åB�]�g�L�A�������s�ƦC����^ ���O���i�������A
�h n=m�A�åB�]�g�L�A�������s�ƦC����^
 ���O�i�f�����C ���O�i�f�����C
- (2)
�Y
 �A
�䤤 �A
�䤤  ,�K, ,�K, �A
�b ���O�D�s�������ơA�B �A
�b ���O�D�s�������ơA�B  ,�K, ,�K, ��⤬��A
�h ��⤬��A
�h
 �Aui �O�i�f�����A �Aui �O�i�f�����A �O�Y�Ӥ����� �O�Y�Ӥ�����
- (3)
�] p �O��ơA�\ �P �] ���O�����ƥB
 �C
�Y �\ ��㰣 p �P �]�A�h p ��i�㰣 �]�C �C
�Y �\ ��㰣 p �P �]�A�h p ��i�㰣 �]�C
- (4)
�] n �P m �O��ơC�Y n �P m �b��Ƥ�������A�h n �P m �b
![$\mathbf{Z}[\omega]$](img46.gif) �����]����C �����]����C
- (5)
�Y �\ �O���N�����ơA�h���i�D�o�@�Ӿ�� n�A�ϱo
-
- ����
�Ĥ@�өʽ誺�ԭz�A�ڭ̤���g��
 �A
�]���n������ �A
�]���n������
�����Υ]�A�b���C�ܩ���ҩ��A�u�n��L��H�N�ƪ��H���ܮe���A�ѡ]���ҩ�
![$\mathbf{Z}[\omega]$](img46.gif) �O�ڤ����^�C
�ĤG�өʽ��ح��A�P�˪��h�X�i�f���� ui�C
�Ҥl�A �O�ڤ����^�C
�ĤG�өʽ��ح��A�P�˪��h�X�i�f���� ui�C
�Ҥl�A ���O�����ߤ�A���O ���O�����ߤ�A���O
�o�өʽ誺�ҩ��ˬO�ܮe���C(�Q�Ωʽ�(1))
�ĤT�өʽ誺�ҩ����e���A�n�Q�Ψ��� p �b������������(ramified)���ʽ�C
�ĥ|�өʽ誺�ҩ�:
 �F�Y �\ �O�㰣 n �P m �������ơA
�h �\ �㰣1�C�G �\ �O�i�f�����C �F�Y �\ �O�㰣 n �P m �������ơA
�h �\ �㰣1�C�G �\ �O�i�f�����C
�n�ҩ��Ĥ��өʽ�A�Y �\ �P �] �O�����ơA�b�� 3 ���U�A
�]���A�b
 �ɡA �ɡA
�Y�A�� n=p3+q3 �Y�i�C
�{�b�i�H�ҩ��w�z 3�C
�w�� x3+y3 =z3�Az �O���ơAx �P y �O�_�ơC�Ҽ{
- ���p 1�G
z-y�A�P
 �����]�� �\�A�\ �O���i���C �����]�� �\�A�\ �O���i���C
�h �\ �㰣
�P�z�A�\ �㰣  �C
�� y �P z ����A �G y �P z �b �C
�� y �P z ����A �G y �P z �b
![$\mathbf{Z}[\omega]$](img46.gif) �]����]�ʽ�(4)�^�C
�o �\ �㰣 �]����]�ʽ�(4)�^�C
�o �\ �㰣  �C�� �C��
 �C
�G �\ �㰣 �C
�G �\ �㰣  �A�]���]�㰣 3�C�� �\ �S�㰣 z-y�C �G 3 �㰣 z-y �]�ʽ�(3)�^�C
�o�� 3 �㰣 x3�C �o�ҡC��L�����Ūp�i�馹�B�z�C �A�]���]�㰣 3�C�� �\ �S�㰣 z-y�C �G 3 �㰣 z-y �]�ʽ�(3)�^�C
�o�� 3 �㰣 x3�C �o�ҡC��L�����Ūp�i�馹�B�z�C
- ���p2
z-y,
 , , ��⤬��C ��⤬��C
 �Au �O�i�f�����A
�\ �O�����ơ]�ʽ�(2)�^�C �Au �O�i�f�����A
�\ �O�����ơ]�ʽ�(2)�^�C
�G
 ���O�i�f�����u��
���O�i�f�����u�� 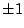 �A �A �A �A �C
�G �C
�G
 �A
k= 0,1,2
��10
�C
�b�� 3 ���U�A �A
k= 0,1,2
��10
�C
�b�� 3 ���U�A
 �A
�]���A �A
�]���A
 �C
�G�X �C
�G�X
 �o
�o
�N k=0,1,2�A�Q��
�i��
 �C �C
k=1 �ɸ������A�G�u�N�����p�Q�סC��
�G
 �A�P�z�A��
y3 = z3 - x3 �i�o �A�P�z�A��
y3 = z3 - x3 �i�o
��
�Y
 �A�h �A�h
 �A
�N�����Y�N�J
x3 + y3 = z3�C�G �A
�N�����Y�N�J
x3 + y3 = z3�C�G
3 z3 -9z2(s+t) + 27z(s2 +t2) -27(s3+t3) = 0
�i�� z �O 3 �����ơC
�����H�W����k�ALagrange�BGauss�BJacobi�BKummer �����ϥιL�A��̤j�S�I�O��Ƽ� �s �ޤH��ƽת���s�CŪ�̤����Q�@�U�A�p�G��  �ޤJ��{��
x2 + y2 = z2 ����s�A���G�p��H
��11 �ޤJ��{��
x2 + y2 = z2 ����s�A���G�p��H
��11
���M�A�̤j�x�������٤��u�p���C
Peter Gustav Lejeune Dirichlet�]1805��l859�^�~����R����k�ޤJ��ƽת���s�A
���G�O���ߤF�ѪR�ƽ� (analytic number theory) ����¦�CDirichlet �@�Ӧ��W���w�z�O�A�Y a �P n �O�����ơA�h������ nl+a ����Ʀ��L�a�h�ӡC
|
|
|





