我們先討論 xⁿ + yⁿ = zⁿ 的整數解的基本性質。

性質 1 如果 x, y, z 是滿足 xⁿ + yⁿ = zⁿ 的整數，且 x, y, z 三數的最大公約數是 1， 則 x, y, z 兩兩互質。
理由：若 e 是 x 與 y 的最大公約數，且 e>1，則 e 整除 xⁿ + yⁿ = zⁿ，故 e 與 z 不會互質。矛盾。

性質 2 若 x, y, z 是滿足 xⁿ + yⁿ = zⁿ 的整數，則必可找到另一組整數 u, v, w， 使得 uⁿ + vⁿ = wⁿ，且 u, v, w 兩兩互質。
理由：令 d 是 x, y, z 的最大公約數， , , 。

性質 3 若 p 與 m 是正整數，且 x^p + y^p = z^p 沒有全異於零的整數解，則 x^pm + y^pm = z^pm 也沒有全異於零的整數解。

性質 4 要解決 Fermat 問題只需證明： xⁿ + yⁿ = zⁿ 沒有全異於零的整數解， 其中 n=4 或奇質數（不為 2 的質數）。
理由：任何一個大於 2 的整數必有一個因數是 4 或奇質數。

現在我們要找出 x² + y² = z² 的所有整數解。

定理 1 x² + y² = z² 的互質整數解為 x=2uv, y=u²-v², 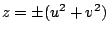， 其中 u, v 是任意互質整數，且 u, v 不同時為奇數。

證明 1 令 x, y, z 是互質正整數，且 x² + y² = z²。若 x 與 y 都是奇數，則 z 是偶數。故 x² + y² 是 4l+2 的型式，z² 是 4l' 的型式（l 與 l' 是整數）。矛盾。

因此，不妨假定 x 是偶數，y 與 z 是奇數。

由 x² = z² - y² = (z+y) (z-y)，令 x=2r, z-y = 2s, z+y = 2t。得 r² = st。

s 與 t 互質，因 y 與 z 互質。但 st 是完全平方。故 s=u² , t=v²。得證。

證明 2 x² + y² = z² 的正整數解對應於 A²+B²=1 的正有理數解。 A² + B² =1 的參數方程式是 ， 。把 T 用 代入， 得 x=2uv，y=u² - v²，z = u² + v²。利用以上的想法，讀者請自己寫出一個完整的證明 ^註7 。

討論：證明 2 其實是把 x² + y² = z² 的整數解看成代數曲線上的有理點。在本文第 5 節還會介紹第三種證明方法。 這個定理雖然很簡單，我們卻不厭其煩的提出三個證明，原因是， 第一個證明是算術的方法，第二個證明是從代數曲線的角度來進行的， 第三個證明是從代數數論的角度來進行。