數論在密碼上的應用 (第 3 頁)

　1│2│3│4│5│6　

數論在密碼上的應用（第 3 頁）

楊重駿;楊照崑

首頁 | 搜尋

．原載於數學傳播第七卷第二期、第七卷第三期
．作者當時任教於美國海軍研究實驗所;美國佛羅里達大學統計系
‧對外搜尋關鍵字

三、狄飛、赫爾曼、麥克兒(Diffie, Hellmon, Merkle)法

此法是由上列三位電機工程師兼數學家（科學本是一家，觸類旁通，稱他們是什麼家並不正確，也不重要），在1976及1978年所發表的方法。在此方法中，所有的信號必須寫成二進位的形式，例如前面的我字代碼3314,若以二進位表示則為

$\begin{displaymath}2^{11}+2^{10}+0\cdot 2^9+0\cdot 2^8+2^7+2^6+2^5+2^4+0\cdot 2^3+0\cdot 2^2+2^1+0\cdot 2^0\end{displaymath}$

即

110011110010

我們將任何一位信號分成許多段，每段含n個0與1的數，即(x₁，x₂，…，x_n)，以下是本密碼法的收發程序(參看圖1)

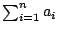1.由收報者秘密的取一組滿足定理2.4的正整數列(a₁，a₂，…，a_n)及任一大於 $\sum_{i=1}^n a_i$ 的質數m，及另一數w，令

$\begin{displaymath}a_i^0\equiv a_iw(\mbox{mod}\, m)\end{displaymath}$

2.(公開)發出(a₁⁰,a₂⁰,…,a_n⁰)給發報者(敵方可以知道)

3.發報者用a₁⁰，a₂⁰，…，a_n⁰與要發的0，1信號x₁，x₂，…，x_n,求出

$\begin{displaymath}c^0=\sum_{i=1}^n x_ia_i^0\end{displaymath}$

並將c⁰之值告訴發報者(敵方可以知道c⁰)

4.收報者收到c⁰之後，可以解出原信號x₁,x₂，…，x_n(而敵方卻不容易用已知的a₁⁰，a₂⁰，…，a_n⁰及c⁰解出信號，原因馬上會談到)。

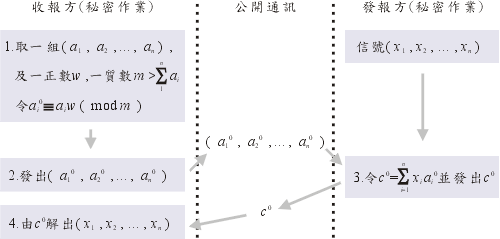
圖1 在此種操作中，敵方僅知（a₁⁰,…,a_n⁰）及 c⁰，而發方除了自己的信號外並不比敵方多知道什麼密碼的機密；只有發方完全掌握了解碼的方法。

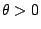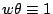我們先看收方如何解出x_i，由定理2.2之系可知存在一 $\theta >0$ 且 $w\theta\equiv 1$ (mod m)若將收到之信號方程式兩邊乘以θ可使

$\begin{displaymath} c^0=x_1a_1^0+x_2a_2^0+\cdots +x_na_n^0 \eqno{(3.1)} \end{displaymath}$

變成

$\begin{displaymath} c^0\theta =x_1a_1^0\theta +x_2a_2^0\theta +\cdots +x_na_n^0 \theta \eqno{(3.2)} \end{displaymath}$

但

$\begin{displaymath}a_i^0\theta\equiv a_iw\theta\equiv a_i(\mbox{mod}\, m)\end{displaymath}$

故令

$\begin{displaymath}c^0\theta\equiv c(\mbox{mod}\, m)\end{displaymath}$

(3.2)即成為

$\begin{displaymath}c\equiv x_1a_1+x_2a_2+\cdots +x_na_n(\mbox{mod}\, m)\end{displaymath}$

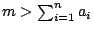因 $m>\sum_{i=1}^n a_i$ ，上式與c=x₁a₁+x₂a₂+… +x_na_n相同，根據定理2.4之說明，一下子就可以解出x₁，x₂，…,x_n可是敵方在整個的過程中知道(3.1)之關係，因a_i⁰並不見得是一個有a_i那樣規則的數列，到目前為止只有硬試一途，即

$\begin{displaymath}(x_1,\cdots ,x_n)=(1,0,0,\cdots ,0),(0,1,0,\cdots )\end{displaymath}$

等一個一個的試，對小的n這並不難，但對大的n而言，譬如說n=1000(這並不是一個很長的信號)，則平均要試2^1000-1=10³⁰¹次才可以解開，這是一個天文數字，若電腦在一秒鐘內可以做一百萬次檢驗(目前尚辦不到) ，則一年只可以做 3.15 x 10¹³檢驗，那麼要解開(3.1)需要10²⁸⁸年，前面談過地球的年齡不過5 x 10⁹年而已，我們且舉一個簡單的例子。

例：令n=5,(a₁，a₂，a₃，a₄，a₅)=(1,3,6,12,25)，w=13，m=51，則收方發出的密碼法(a₁⁰，a₂⁰,a₃⁰，a₄⁰，a₅⁰)分別為

$\begin{displaymath} \begin{eqalign} a_1^0 &\equiv 13\times 1 \equiv 13 \pmod{51}... ...\\ a_5^0 &\equiv 13\times 25 \equiv 19 \pmod{51} \end{eqalign}\end{displaymath}$

這即是發報者收到的作密碼的a⁰，假定發方所要發的情報是10101，則因

c⁰=13+27+19=59

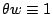故收方所收到的密碼是59，要解開此碼，收方先得找到θ使 $\theta w\equiv 1$ (mod 51)。用輾轉相除法很快得到θ=4，故收方所要解的是

$\begin{displaymath} c\equiv 59\times 4\equiv 32 \pmod{51} \end{displaymath}$

即

32=x₁+3x₂+6x₃+12x₄+25x₅=1+6+25

即原信號為10101，至於敵方所要解的是

59=13x₁+39x₂+27x₃+3x₄+19x₅

這自然不算太難，但我們可以看見 a_i⁰ 失去了任何規則，當 n 很大時就不容易解開了。

　1│2│3│4│5│6　


	（若有指正、疑問……，可以在此留言或寫信給我們。）

EpisteMath (c) 2000 中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有

編輯：陳文是 ∕ 繪圖：簡立欣

最後修改日期：6/17/2002