���~�ǤH�ۿ˰O �]�� 2 ���^
���v��
�D�����ƾǶǼ��ĤG���ĤT��
�D�@�̷��ɥ��Щ��ƾǨt
�E����
�E��~�j�M����r
|
���~�ǤH�ۿ˰O �]�� 2 ���^ ���v��
|
�D�����ƾǶǼ��ĤG���ĤT�� �D�@�̷��ɥ��Щ��ƾǨt �E���� �E��~�j�M����r |
�{�b�� n ��Өq�A�Ʀn���ǡA�@�@�X�{�g�e�C�ڤw���L�A�ڭ̰��]�o�̦U�����P���W���A�]n �i�d���U�Ҽg�������U�����P�A�̰������Ĥ@�W�A�����̲ĤG�W�K�K�^�C�ڭ̥H xk �N���� k ��Өq���W���]�Τ���ڦW���A�Y�o�b n �줤��O�ѴX�^�Cxk �O�@�ӡu�ð��ܼơv�]=�u�H���ܼơv�^�C�ڤ]���L�A�o�̨C�쪺�W���A�A�@�L�Ҫ��C�A�Ҫ��D���A�O�C�쪺�{�ɦW���A�]�N�O���A�A�ݨ�� k ��ɡA�o�b�Ҭݧ��� k �줤�A��O�ѴX�C �e����²���k�]�u���e�@�b�K�K�v�^�A���G�w�g�D�`�����C�]���ڭ̦۵M�a�|�Q���@��@�I����k 3 �G
Mr�G���e�� k-1 ��C�۲� r ��_�A�����J����e���Ϊ̧Y���C
�]�N�O���A�۲� r ��_�A��ܭ����X�{���{�ɲĤ@�W�C�Ъ`�N�A�ҿש��e�� r-1 ��A���M�O�A�M����o�̡A�]�i�������W�I�^�A���O�A������o�̨C�쥴�q�@�f�A�H�K�P��Ӫ��@�Ӥ���A�]�N�O���A�H�K�M�w��Ӫ̪��{�ɦW���C�S M1�A�S������N��G�A��������Ĥ@��A�]���Ĥ@��@�w�O�@���{�ɲĤ@�W�C �ڭ̳W�w�@��ӲŸ��A�ϤU�����ԭz��K�ǡC�O
P(Mr) ���ھڤW�z��k�A�襤�Ĥ@�W�����v
Sk ���ھڤW�z��k�A�� k ��Өq�Q�諸�ƥ�
����]������H�^
�o�� P(A,B) �N�� P(A �B B)�C��M�A
�ڭ̲{�b�n�ˬd�@�U�A�b�W�z��k�ءA���@��r���P(Mr)�̤j�C
��o��r�s��r*�A����Mr*�N�O�̨Ϊ���ܪk�C�ݨ�o�ءA
����Ӥߤ@�I��Ū�̤]�\�|�ݡG�A���i�H�O�ҨS���A�n����k�O�H���y�ܻ��G�̦n����k�A�@�w�O�b�W�z�o��
�ѳo�اA�i�H�`�N��A
�o�ئ��쪺�O�A���M r* �H n ���ܡA���� n �ܤj�ɡA
�p�G�ڭ̤�����n�A�p��3�B��4�A�A�N�i�H�ݥX
�G
�Ϊ̻�
�ھ�(5),
�]�� �o�ɭԪ�f(r*)�j���O 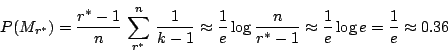
�H�d�ǤH���T�Q��Өq�ӻ��Ar*�j���O11�A�̦n����k�O�u���e10��
|
|
|
|
|
�]�Y�������B�ðݡK�K�A�i�H�b�� �d�� �� �g�H ���ڭ̡C�^ |
|
|
|
EpisteMath (c) 2000 ������s�|�ƾǩҡB�x�j�ƾǨt �U�����峹���e���ۧ@�v����ۧ@�H�Ҧ� |
| �s��G�x�� | �̫�ק����G4/26/2002 |