認識連分數 (第 6 頁)

　1│2│3│4│5│6│7　

認識連分數（第 6 頁）

林聰源

首頁 | 搜尋

．原載於數學傳播第二卷第三期
．作者當時任教於清大數學系
‧對外搜尋關鍵字

§5. 連分數的應用（實例說明）

[例 1] （圓周率）的連分數表示為 $[\, 3,7,15,1,292,1,1,\cdots \, ]$ ，代入公式 1 得

$\begin{eqaligntwo*} p_0 &= 3 & q_0 &= 1 \\ p_1 &= 7\times3+1=22 & q_1 &= 7 \\ ... ...& q_3 &= 1\times106+7=113 \\ p_4 &= 103993 & q_4 &= 33102 \\ \end{eqaligntwo*}$

故得出其頭幾個漸近分數為 3/1, 22/7, 333/106, 355/113，……我國在紀元五世紀時，祖沖之即以 22/7 為「疏率」（比π之實際值略大），以 333/106 為「密率」（比 π 之實際值略小）。由推論 2，

$\begin{displaymath} \left\vert \pi-\frac{355}{113} \right\vert \leq \left\vert ... ...13} \right\vert \leq \frac{1}{113\times33102}<\frac{1}{10^5}, \end{displaymath}$

可知以 355/113 為 π 的近似值時準到小數點後面 6 位。事實上，祖沖之求出

$\begin{displaymath}3.1415926<\pi<3.1415927,\end{displaymath}$

這是數學史上極光輝的貢獻。

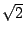[例 2] 16世紀的時候，義大利數學家 Bombelli 利用連分數求 $\sqrt{2}$ 的近似值，他的做法如下：

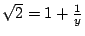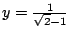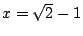令 $\sqrt{2}=1+\frac{1}{y}$ ，則 $y=\frac{1}{\sqrt{2}-1}$ ，今以 $x=\sqrt{2}-1$ 代入，則

$\begin{eqnarray*} x = \frac{1}{y} &=& \frac{1}{\sqrt{2}+1} = \frac{1}{2+x} \\ ... ...r1.5ex\hbox{$+$}\; \frac{1}{2} \; \lower1.5ex\hbox{$+$}\; \cdots \end{eqnarray*}$

它的頭幾個漸近分數為

$\begin{displaymath} \frac{1}{2},\frac{2}{5},\frac{5}{12},\frac{12}{29},\frac{29}{70},\frac{70}{169},\frac{169}{408},\frac{408}{985},\cdots \end{displaymath}$

而

$\begin{displaymath} \left\vert (\sqrt{2}-1)-\frac{169}{408} \right\vert \leq \frac{1}{408\times985}<\frac{1}{4\times10^5}, \end{displaymath}$

這就說明了以 1+(169/408) 做為 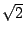$\sqrt{2}$ 的近似值時，誤差小於四萬分之一。

[例 3] 閏年的算法。現在通行的辦法是每四年一閏，每逢百年免閏一次，而每逢四百年又恢復一閏，另外還有「閏秒」的鮮事。用連分數的方法來看就清楚了：

地球繞日一周需時365天5時48分46秒，以天為單位化成分數即

$\begin{displaymath} 365+\frac{5}{24}+\frac{48}{24\times60}+\frac{46}{24\times60\times60} =365\frac{10463}{43200} \end{displaymath}$

將分數部分 10463/43200 展成連分數。（下面的直算式為輾轉相除法的簡寫型式）得出

$\begin{displaymath}\frac{10463}{43200} = \frac{1}{\displaystyle 4 + \frac{1}{\... ...isplaystyle 3 + \frac{1}{\displaystyle 5 + \frac{1}{64}}}}}} \end{displaymath}$

$\begin{displaymath} \begin{tabular}{rr\vert c\vert rl} \multicolumn{2}{r\vert}{\... ...line{\, 64 \,} & 64 & 1 & \\ \cline{2-2} & & & & \end{tabular}\end{displaymath}$

其中

a₀=0,a₁=4,a₂=7,a₃=1,a₄=3,a₅=5,a₆=64

由公式 1

$\begin{eqnarray*} && p_0=0, \; p_1=1, \; p_2=7, \; p_3=8, \; p_4=31, \; p_5=163... ...1=4, \; q_2=29, \; q_3=33, \; q_4=128, \; q_5=673, \; q_6=43200 \end{eqnarray*}$

其最佳漸近分數依次為

$\begin{displaymath} \frac{1}{4},\frac{7}{29},\frac{8}{33},\frac{31}{128}, \frac{163}{673},\frac{10463}{43200} \end{displaymath}$

（愈後愈佳），頭一個漸近分數 1/4 告訴我們每四年一閏，第三個漸近分數 8/33 告訴我們每三十三年八閏，換句話說，每九十九年二十四閏，而與我們現行的辦法，為方便計，定為每一百年二十四閏相差極微，若每四年一閏，則每百年有二十五閏，故需略作調整，這就是逢百不閏的道理。每四百年間，有三段 128 年，另加 4 段 4 年，故閏年的總數該為 3 x 31 + 4 x 1 = 97，若每百年 24 閏則 400 年有 96 閏，比實際需要的少了一次，故需再作調整，這就是逢 400 年恢復閏年的理由。

以上所述，牽涉的數字像 100,400 是人為的（為了方便記憶），按學理講，更正確的閏年表應如下列：（括號表示閏年，請注意逗點的位置與漸近分數分母的關係。）

1	2	3	(4),	5	6	7	(8),	9	10
11	(12),	13	14	15	(16),	17	18	19	(20),
21	22	23	(24),	25	26	27	(28),	29,,	30
31	32	(33),,,	34	35	36	(37)	38	39	40
(41)	42	43	44	(45)	46	47	48	(49)	50
51	52	(53)	54	55	56	(57)	58	59	60
(61)	62	63	64	65	(66),,,	67	68	69	(70)
71	72	73	(74)	75	76	77	(78)	79	80
81	(82)	83	84	85	(86)	87	88	89	(90)
91	92	93	94	(95)	96	97	98	(99),,,	100
101	102	(103)	104	105	106	(107)	108	109	110
(111)	112	113	114	(115)	116	117	118	(119)	120
121	122	(123)	124	125	126	(127)	128,,,,

讀者可從上圖明顯看出它與習俗上曆法之差別處；在現行曆法中，夏至、冬至的日子常因年份而提前或挪後一天（通常冬至為12月22日），如果採用上圖，就可大大省略這種麻煩，但上圈的規則不便記憶，所以不太可能實行。

[例 4] 陰曆閏年的由來是因為月球繞地球一周需時 29.5306 天（即朔望的週期），而一年（地球繞日的周期）是 365.2422 天，兩數相除得 365.2422/29.5306=12.37，所以一年該有 12.37 月，此數非整數，只得以 12 個月為一年，而將尾數 0.37 累積成閏月。今將 0.37 展成連分數

$\begin{displaymath} 0.37 \; = \; \frac{1}{2} \; \lower1.5ex\hbox{$+$}\; \frac{1}... ...hbox{$+$}\; \frac{1}{1} \; \lower1.5ex\hbox{$+$}\; \frac{1}{3} \end{displaymath}$

其漸近分數依次為：

$\begin{displaymath} \frac{1}{2},\frac{1}{3},\frac{3}{8},\frac{7}{19},\frac{10}{27} \end{displaymath}$

而閏年（即有閏月之年）應如下安排：（括號表示閏年）

1	(2),	3,,	4	(5)	6,,	7	(8),,,	9	(10)
11	12	(13)	14	15	(16),,,	17	(18)	19,,,,	20
(21)	22	23	(24)	25	26	(27),,,,,

我們可從上圖清楚地看出來，每隔兩年或三年出現一次閏月。

[例 5] 陰曆月大月小的由來是因為月球繞地球一周需時 29.5306 天，此數非整數，若以 29 天為一個月，則顯太少（是為小月），若以 30 天為一個月則顯太多（是為大月），至於其間安排的規則也可根據連分數理論找到線索，其法如下：

將 0.5306 展成連分數，則得（其算式如下圖）

$\begin{eqnarray*} 0.5306&=&\frac{5306}{10000}=\frac{2653}{5000} \\ &=& \frac{1... ...1.5ex\hbox{$+$}\; \frac{1}{33} \; \lower1.5ex\hbox{$+$}\; \cdots \end{eqnarray*}$

$\begin{displaymath} \begin{array}{r\vert c\vert r} & & 5000 \\ 2653 & 1 & 265... ...-3} \underline{\, 2 \,} & 2 & 1 \\ \cline{1-1} & & \end{array}\end{displaymath}$

由此可直接寫出下表（括號表示月大，請注意同一逗點符號出現之次數與 a_k 間的關係）

$\begin{displaymath} \begin{array}{llllllllll} (1),&2,,&(3)&4,,&(5)&6,,&(7)&8,,&(... ...9)&40\\ (41)&42&(43)&44&(45)&46&(47)&48&(49),,,,,& \end{array}\end{displaymath}$

讀者不難看出前 12 個月大小月間隔整齊，六大六小，其次的 12 個月則為 7 大 5 小等等。我曾拿這個表和今年的月曆對照，發現它上面居然有連續兩個大月，也有連續兩個小月的情形，令我困惑不已，難道說其中另有人為的因素嗎？讀者不妨驗證一下。

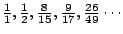（註：漸近分數為 $\frac{1}{1}, \frac{1}{2}, \frac{8}{15}, \frac{9}{17}, \frac{26}{49} \cdots$ ）

　1│2│3│4│5│6│7　


	（若有指正、疑問……，可以在此留言或寫信給我們。）

EpisteMath (c) 2000 中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有

編輯：李渭天 ∕ 繪圖：簡立欣

最後修改日期：4/26/2002