冪級數

Power Series

  

 

冪級數在微積分中是個重要的題材，許多重要的函數可表成冪級數，而冪級數全體也代表了相當廣泛的函數類別。

冪級數形式上是個無窮多項式，通常依變數 x 的升冪順序來表示： $a_0 + a_1 x + a_2 x^2 + \cdots + a_n x^n + \cdots$ （更一般，則以 x-x0 代替 x0xA141x0 為一固定的數。） 冪級數之間的四則運算就像多項式那樣，而函數在其冪級數表示的絕對收斂範圍內，要求其積分與微分也很簡單，只要分項求其積分與微分，再做線性和就好。Newton 式的微積分可說就是冪級數式的微積分，因為他善用廣義（指數可為分數）二項式展開式，把重要函數都寫成冪級數，再求微分與積分。

在 Newton 的影響下，有一陣子大家把函數等同於冪級數，後來才發現有些函數無法用冪級數表示，而要動用到三角級數或者函數項級數才能表示，有些甚至連廣義的級數也無法表示。另一方面，函數能用冪級數表示，有時也要限制變數 x 的適用範圍，譬如

\begin{displaymath}\sin x = x - \frac{1}{3!}x^3 + \frac{1}{5!}x^5 - \cdots\end{displaymath}

對所有 x 都成立，但

\begin{displaymath}\tan^{-1} x = x - \frac{1}{3} x^3 + \frac{1}{5} x^5 - \cdots \end{displaymath}

卻只有當 $ -1 \leq x \leq 1 $ 時，才成立。

處理函數冪級數表示的一重要課題就是決定適用的範圍。Taylor 定理說，在適當的條件之下， f(x) 可寫成為

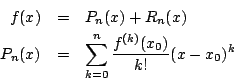
\begin{eqnarray*} f(x) & = & P_n(x) + R_n(x) \\ P_n(x) & = & \sum^{n}_{k=0} \frac{f^{(k)}(x_0)}{k!} (x-x_0)^k \end{eqnarray*}


稱為 f(x) 在 x0 的 n 階 Taylor 多項式。 Rn(x) 則稱為於餘項，其表現法也是一個重要的課題。如果對某個 x 值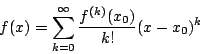， $ \lim_{n \rightarrow \infty} R_n(x) = 0 $，則 $f(x)= \lim_{n \rightarrow \infty} P_n(x) $，亦即 f(x) 在此 x 值有如下的冪級數表示：

\begin{displaymath}f(x) = \sum^{\infty}_{k=0} \frac{f^{(k)}(x_0)}{k!} (x-x_0)^k \end{displaymath}

所有使此式成立的 x 值，就是 f(x) 之冪級數表示的適用範圍。

關於餘項 Rn 的表示法主要有兩種，微分型餘項與積分型餘項。

微分型餘項為

\begin{displaymath}R_n(x)= \frac{1}{(n+1)!} f^{(n+1)}(\xi) \cdot (x-x_0)^{n+1} \end{displaymath}

ξ 與 n+1 有關，且介於 x 與 x0 之間。而積分型剩餘項則為

\begin{displaymath}R_n(x)= \frac{1}{n!} \int^{x}_{x_0} f^{(n+1)}(t) \cdot (x-t)^n dt \end{displaymath}

用微分型餘項，且取 n=0，則 P0 (x) = f(x0)， $R_0 (x) = f'(\xi)(x-x_0)$，

\begin{displaymath}f(x) = P_0(x) + R_0(x) = f(x_0) + f'(\xi)(x-x_0) \end{displaymath}

它正是 平均變率定理（或稱平均值定理）。反過來，由平均變率定理可推廣而得 Cauchy 定理，而由 Cauchy 定理又可推得帶有為微分型餘項的 Taylor 定理。

用積分型餘項，且取 n=0，則 P0(x) = f(x0)， $ R_0(x) = \int^{x}_{x_0} f'(t)dt $，

\begin{displaymath}f(x) = P_0 (x) + R_0 (x) = f(x_0) + \int^{x}_{x_0} f'(t)dt \end{displaymath}

它正是微積分基本定理。反過來，由微積分基本定理，經一再使用分部積分的技巧，就可推得帶有積分餘項的 Taylor 定理。

如果餘項之值很小，則 Taylor 多項式之值就可以用來做為原來函數值之近似值。通常 n 愈大，或 x 愈接近 x0 ，Rn(x) 就愈小。微積分要處理的是 n，|x-x0| ，|Rn(x)| 三者的大小變化與彼此之間的關係。這樣就可以知道 n 取多大，|x-x0| 取多小時，|Rn(x)| 就有多少，因此就可知用多項式 Pn(x) 之值來代替函數值 f(x) 會有多準。

以上都是從函數出發，看它如何表成冪級數，反過來從一冪級數出發，則要討論此無窮和有意義的變數範圍，亦即收斂範圍。在收斂範圍內冪級數代表一函數，我們就得更進步研究此函數的性質。承認冪級數為函數，使函數的範圍擴張了許多，其應用性就更強。譬如許多微分方成就可經由假設函數為冪級數而求解。

 
對外搜尋關鍵字：
．平均變率定理
．微積分基本定理
 

（撰稿：曹亮吉／台大數學系）

相關網頁：
數學條目：函數
數學條目：逼近方法
牛頓如何突破微積分學（曹亮吉）　

回頁首
 

留言（若有指正、疑問……可利用這裡留言）

 
EpisteMath

EpisteMath (c) 2000 中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有


編輯：康明軒 最後修改日期：8/30/2001