函數

Function

函數的觀念隨著微積分的發展而演變，直到十九世紀才完全成熟。

伽利略(1564-1642)研究落體運動，發現「一物體在空中下降的距離，與所經過的時間的平方成正比」。「一物體從高度固定的斜板滑落所需的時間與斜坡的長度成正比」，十七世紀的科學革命開始注重自然界的動態現象，因此促使能夠描述動態的函數觀念漸趨成熟。

研究運動也引出更多的曲線，而曲線和函數之間，也經由坐標的引入，變得不可分離。最早的想法認為：一個函數是一個代數式子，只含變數及加減乘除開方等符號。漸漸地，所謂超越（代數的）函數，如三角、對數、指數等等也加了進來，加上種種曲線的研究，由這些函數經四則運算及合成運算可得的所謂初等函數，在十八世紀上半葉就已經非常清楚了。

Newton(1642-1727)等人儘量把函數寫成冪級數，這樣它的微分與積分，就可經由逐項微分與積分來處理。到了十八世紀中葉，數學家乾脆認定函數就是冪級數，而一般的冪級數都可以看成函數。

此時波動問題的興起，使「函數就是冪級數」這種觀念不時遭到挑戰，迫使Euler(1707-1783)承認，波動開始時，弦所成的曲線y=f(x)可以是任意的，只要是連續的，但不一定可用冪級數來表示。到了十九世紀初，Fourier(1768-1830)研究熱傳導時，他發現必須把初期條件f(x)以三角級數展開：

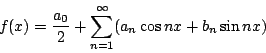
$\begin{displaymath}f(x)=\frac{a_0}{2}+\sum^{\infty}_{n=1}(a_n \cos nx+b_n \sin nx)\end{displaymath}$

而

$\begin{displaymath}a_n = \frac{1}{\pi} \int^{\pi}_{-\pi} f(x)\cos nx dx , b_n=\frac{1}{\pi}\int^{\pi}_{-\pi}f(x)\sin nxdx\end{displaymath}$

根據傳統的作法，他原假定f(x)為冪級數才能有這樣的表示法。但他注意到a_n,b_n只不過是函數 $\frac{1}{\pi}f(x)\cos nx$ , $\frac{1}{\pi}f(x)\sin nx$ 的曲線下的面積而已，所以不管y=f(x)是怎樣的曲線，a_n、b_n都可算得，而深信「任何」函數都可表成三角級數之和。

不過「任何」函數牽涉到函數到底是什麼，這一點Fourier也說不清楚。函數觀念的澄清是Dirichlet(1805-1859)研究Fourier論文後的重要貢獻。他認為函數f是一個規則，它告訴我們變數x之值固定了，其相應唯一的y=f(x)之值是什麼。f不一定要是一個式子，它只要能說明x到y之間的對應是什麼就好了。所以函數不一定是冪級數，也不一定是三角級數；反過來，數學家要研究的是：怎樣的函數可表為冪級數？表成為三角函數？

每一函數都有它的對應規則，這些規則的表現方法至少有三種：式子、圖形、數表， f(x)=x² +x+ 1是個式子，但其實它代表一段敘述，說明x與y=f(x)的對應，只是我們太習慣於多項式所代表的意義，就認為它是個式子。 $f(x)=\sin x$ ，f(x)=[x]（高斯函數）等也一樣，開始時是一段敘述，久了就成為式子。除了「明」的式子外，還有些「暗」的式子。暗的式子指的是以參數函數、隱函數、微分方程式、積分方程式等來表示自變數x與他變數y之間的數學關係（不一定是單值的對應）。怎樣化暗為明自然是重要的課題。

式子之外，函數最常以曲線的形式出現。譬如兩電線桿之間的電線所成的曲線，小提琴的聲波曲線；它們也可用式子表示出來。但像某地的氣溫變化曲線，患病者的腦波曲線等，就很難用式子表示。不過從這些曲線的變化，還是可以對情況有相當的了解。

第三種函數表示法為數表，它使我們馬上查得函數值（或其近似值），這在應用數學上非常重要，而製表的原則及方法則有賴於微積分。（本文節錄自曹亮吉的《微積分》（歐亞書局）之12-3。）

對外搜尋關鍵字：
．Newton
．冪級數
．Euler
．Fourier
．Dirichlet

（撰稿：曹亮吉∕台大數學系）

相關網頁：

數學條目：冪級數

函數觀念的演變史（曹亮吉）


	留言（若有指正、疑問……可利用這裡留言）

EpisteMath (c) 2000 中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有

編輯：鄧惠文

最後修改日期：8/30/2001